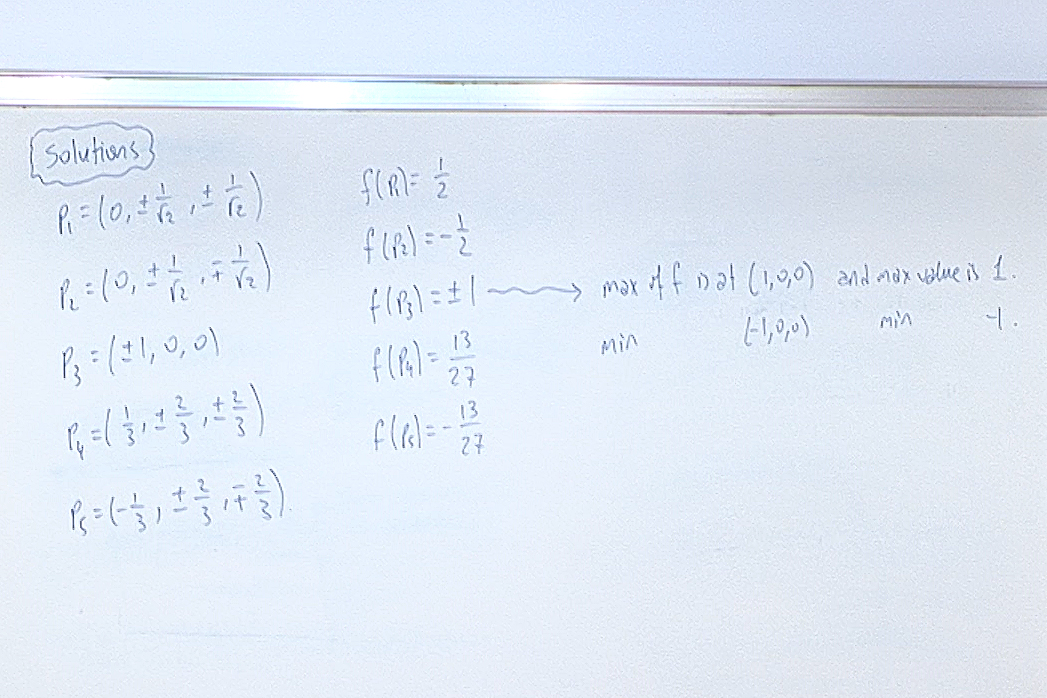Previous Screenshot Next Screenshot
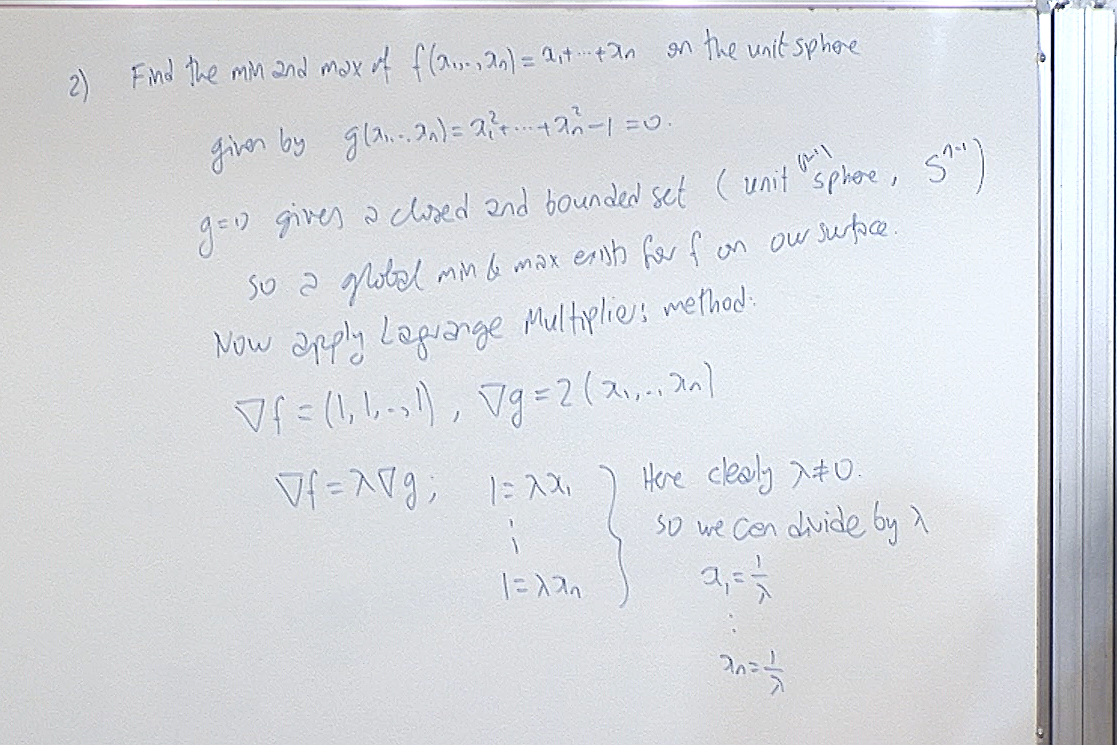
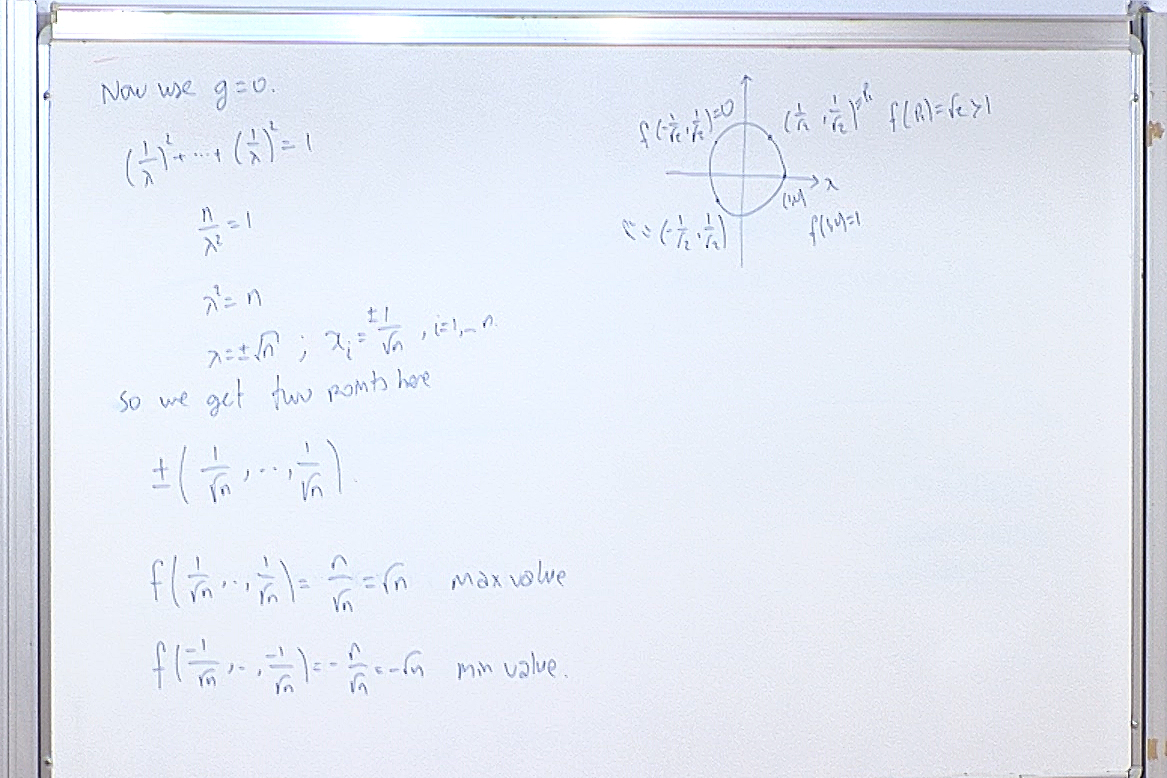




This is how we typically solve the above system of equations.
First assume that $x=0$.
If $y=0$, then from (2) we have $z=0$, but then $(x,y,z)=(0,0,0)$ violates (4), so $y\not=0$.
If $\lambda=0$, from (2) we have $z=0$, which in turn gives $y=0$ from (3) contrary to what we just found about $y$. So $\lambda\not=0$. From (2) it now follows that $z\not=0$ also.
At this point we have $x=0$ and $y,z,\lambda\not=0$.
Joining (2) and (3) we find $z=\lambda y=\lambda^2 z$. Cancelling $z$ from both sides (note that we are using $z\not=0$) we get $\lambda=\pm 1$.
If $\lambda=1$, then from (2) we have $y=z$ and from (4) we get $\displaystyle y=\pm \frac{1}{\sqrt{2}}$.
We obtained the points $\displaystyle p_1=(0,\pm \frac{1}{\sqrt{2}},\pm \frac{1}{\sqrt{2}})$.
If $\lambda=-1$, then from (2) we have $y=-z$ and from (4) we get $\displaystyle y=\pm \frac{1}{\sqrt{2}}$.
We obtained the points $\displaystyle p_2=(0,\pm \frac{1}{\sqrt{2}},\mp \frac{1}{\sqrt{2}})$.
Next assume $x\not=0$.
From (1) we immediately get $\lambda\not=0$.
From (2) we see that either "$y=0$ and $z=0$" or "$y\not=0$ and $z\not=0$".
If $y=0$ and $z=0$, then from (4) we get $x=\pm 1$.
We obtained the points $p_3=(\pm 1,0,0)$.
If $y\not=0$ and $z\not=0$, then as above we can join (2) and (3) to obtain $\lambda=\pm 1$.
If $\lambda=1$, then from (1) we get $\displaystyle x=\frac{1}{3}$.
From (2) we get $z=y$, and from (4) we get $\displaystyle y=\pm\frac{2}{3}$.
We obtained the points $\displaystyle p_4=(\frac{1}{3},\pm\frac{2}{3},\pm\frac{2}{3})$.
If $\lambda=-1$, then from (1) we get $\displaystyle x=-\frac{1}{3}$.
From (2) we get $z=-y$, and from (4) we get $\displaystyle y=\pm\frac{2}{3}$.
We obtained the points $\displaystyle
p_5=(-\frac{1}{3},\pm\frac{2}{3},\mp\frac{2}{3})$.
This detailed analysis of all cases is crucially necessary for finding all the solutions. In particular pay attention before you cancel anything: if what you want to cancel is zero, you cannot cancel but in that case you may find other solutions.