
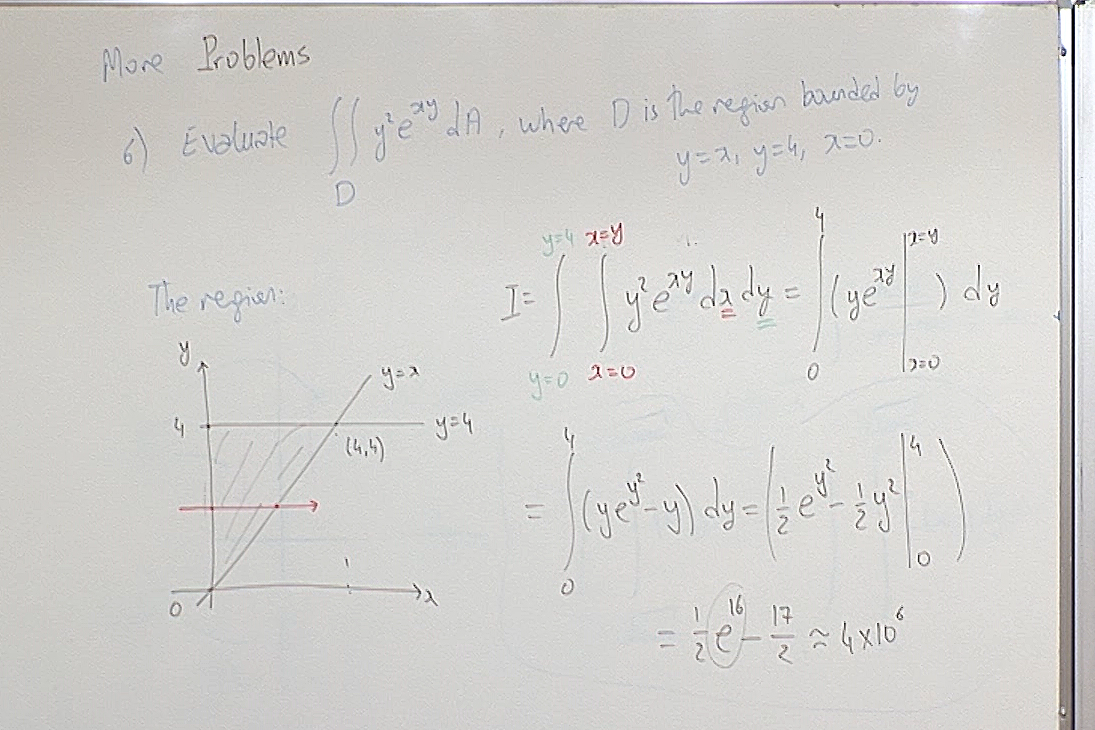
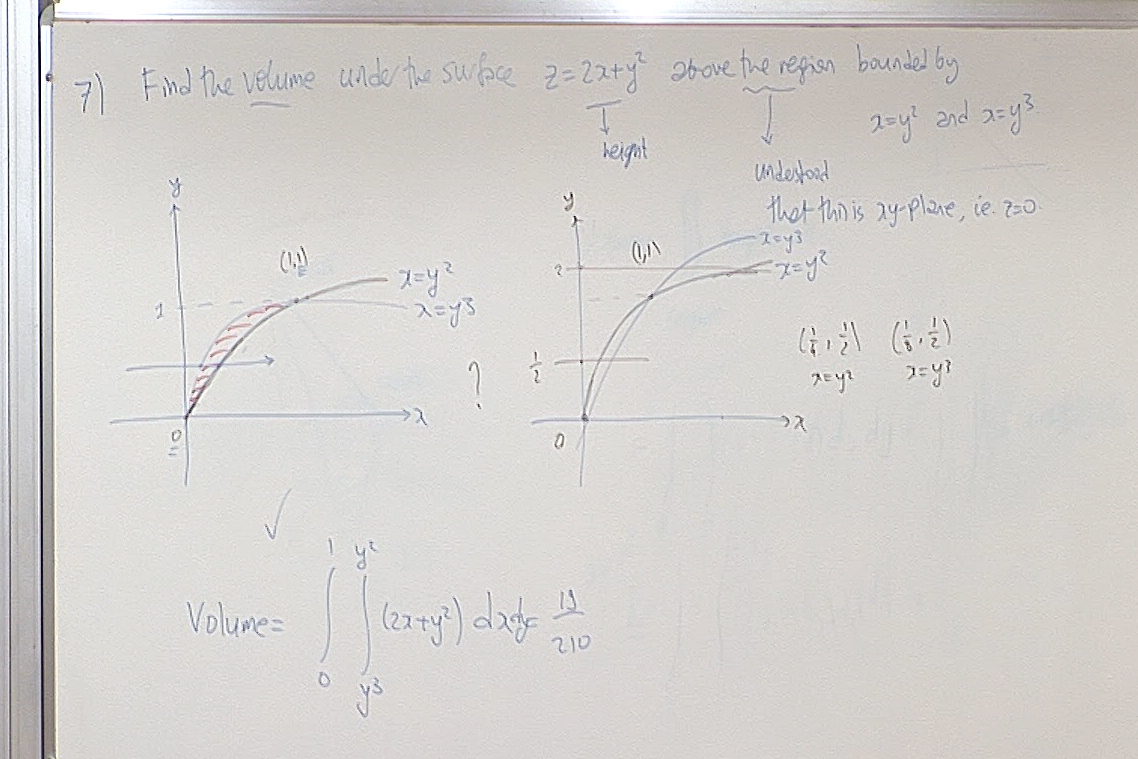
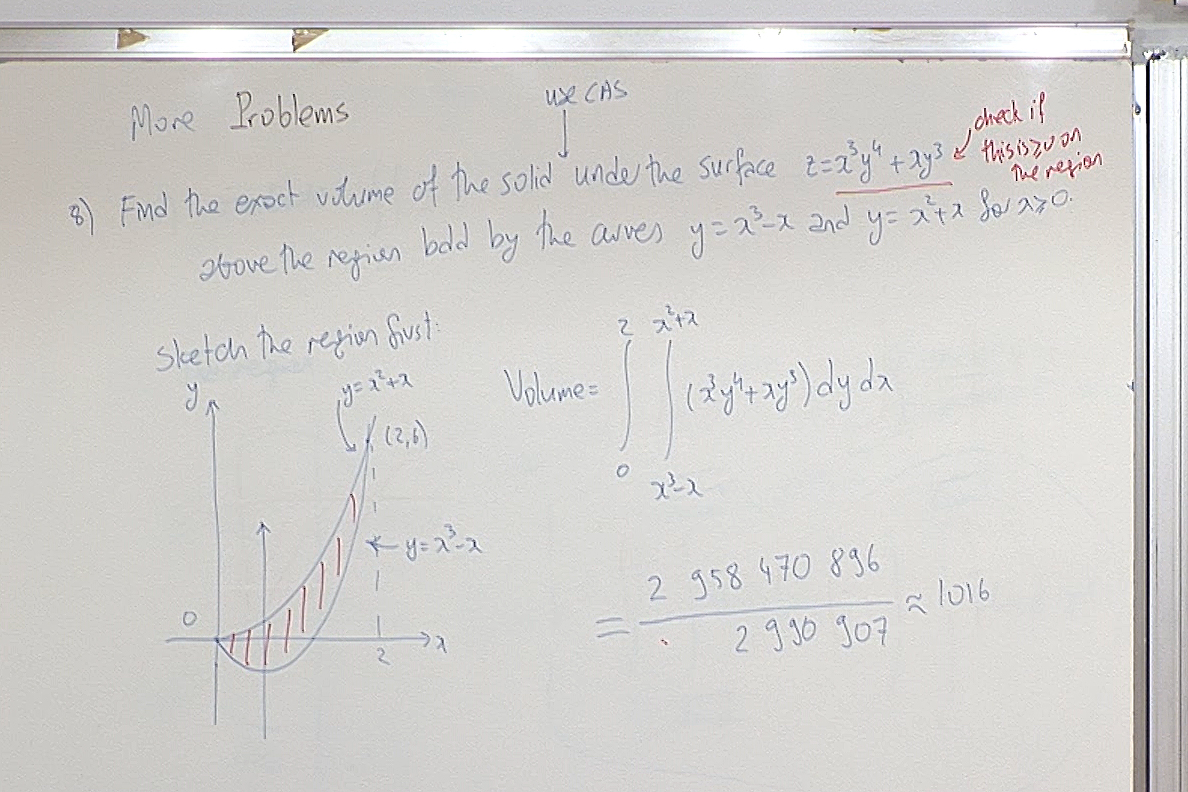
The function $f(x,y)=x^3y^4+xy^3$ is not non-negative on the given region so the "volume" interpretation of this integral is not valid. However it is an exercise in writing the limits of an iterated integral.
Let us check the sign of $f(x,y)$ on the shaded region. When $x,y\geq0$, then clearly $f(x,y)\geq 0$.
It remains to check its sign of $f$ when $0\lt x\leq 1$ and $y\lt 0$. Notice that
\[ f(x,y)=x^3y^4+xy^3=(xy^2)(y)(x^2+1). \]
Note that $xy^2> 0$ and $y\lt 0$ in this region. Hence $f$ will be negative if $x^2y+1>0$. This gives $\displaystyle y\gt -\frac{1}{x^2}$. The lowest point of the shaded region in the figure on the board is the minimum point of $y=x^3-x$ when $x\geq 0$. Taking the derivative, equating to zero we find that $\displaystyle x=\frac{1}{\sqrt{3}}$ and $\displaystyle y=-\frac{2}{3\sqrt{3}}\gt -1$ at that lowest point. Hence this lowest point lies above the graph $\displaystyle y=-\frac{1}{x^2}$ and therefore $x^2y+1>0$ and consequently $f$ is negative on the shaded region below the $x$-axis.
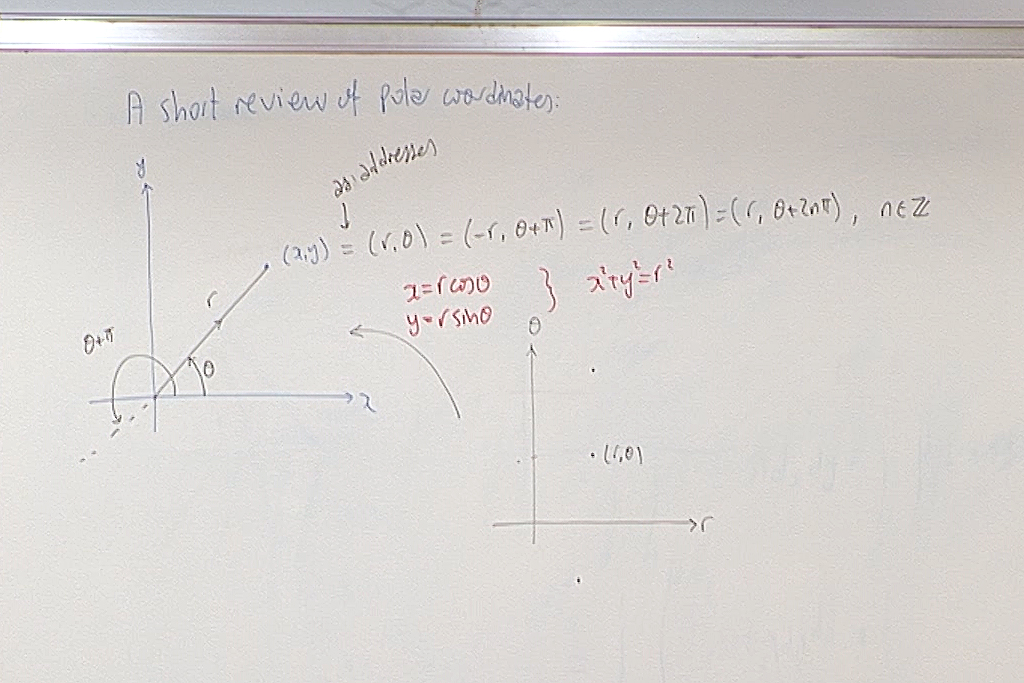
At this point we had a quiz. Here is the question.

