
Previous Screenshot
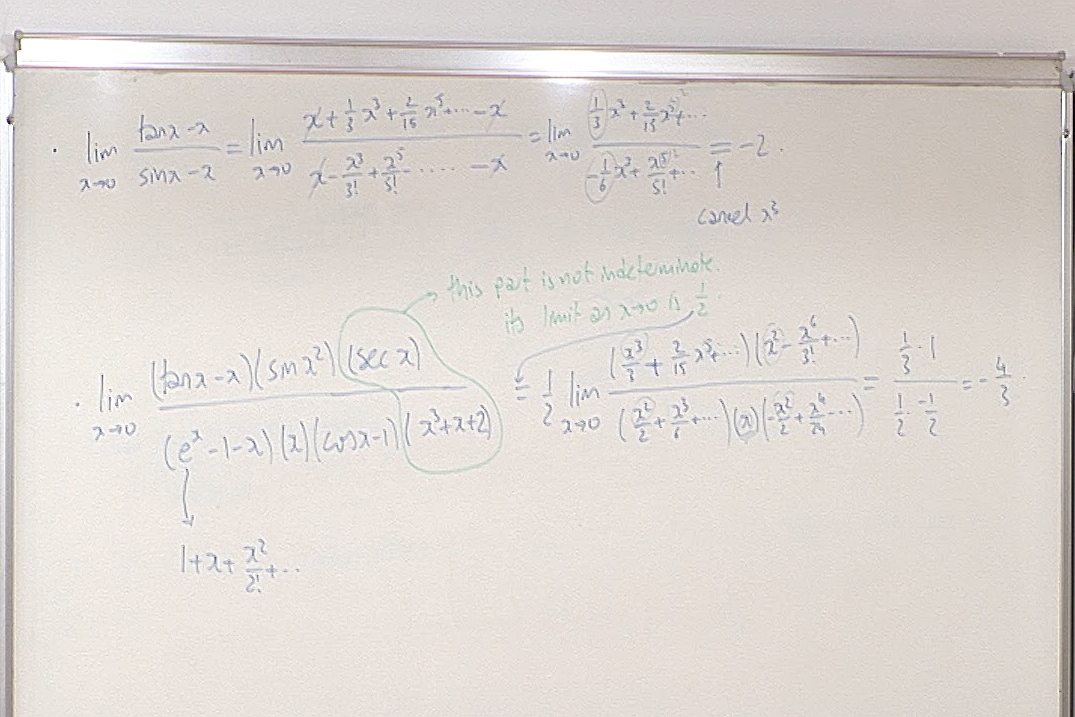
Here I forgot to carry over the factor $\displaystyle \frac{1}{2}$ to the answer, so the correct answer is $\displaystyle -\frac{2}{3}$.



The significance of Machin's formula is that the convergence of the Left Hand Side is now extremely fast as opposed to the convergence of arctan x.
Google "machin type formulas" to see much faster converging series.
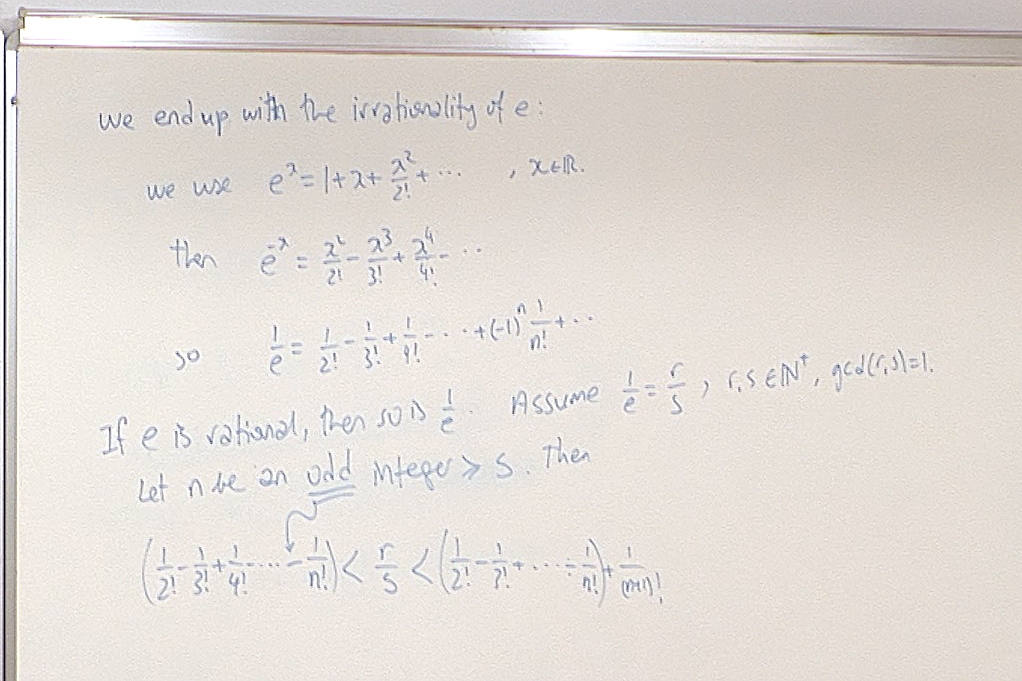

The signficance of transcendental numbers is that there are more transcendental numbers than non-transcendental (algebraic) numbers on the real line, yet it is too complicated to show that a number is transcendental. The proof that e is transcendental is however easy enough to be followed by a Calculus background. That is why it is mentioned here. Just Google "the transcendence of e" and read any of the proofs. Similarly you can also follow a proof of the transcendence of π if you accept that square root of negative one exists!
