
Next Screenshot
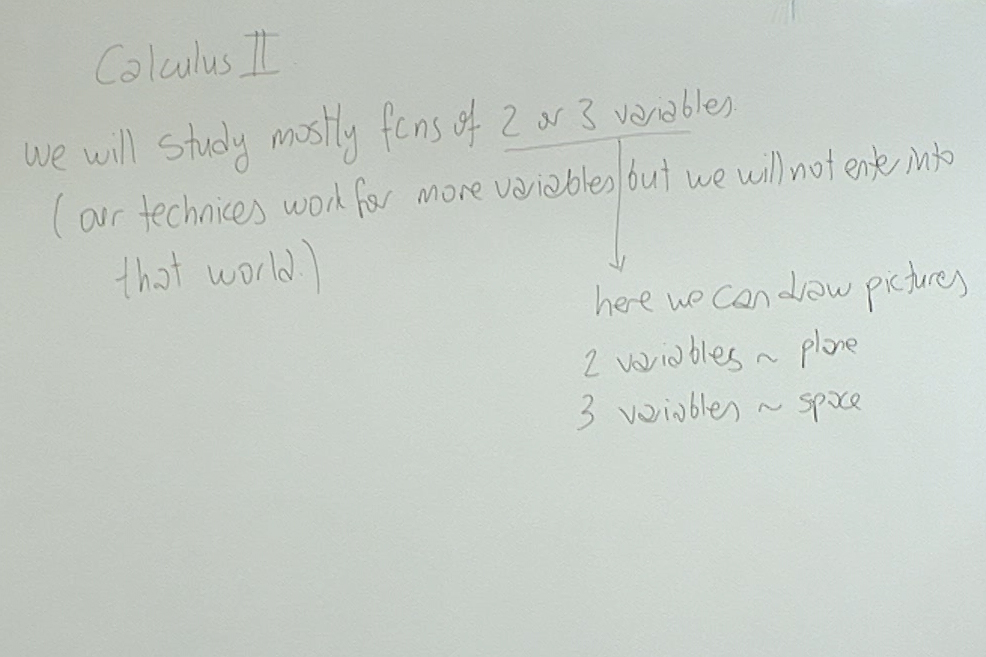
Calculus-II is about real functions of 2 or 3 variables. This allows us to draw nice pictures to stimulate our understanding.
Most of the techniques we develop will be valid in the theory of functions of more than three variables but we will seldom go into that world. The actual theory of functions of several variables, without using any pictures, is done in second year mathematics courses under the name Advanced Calculus.

I will use the notation $p=(x_1,x_2,x_3)$ to denote a point in $\mathbb{R}^3$. This notation has the advantage of being immediately applied to higher dimensions.
The vector notation $p=x_1\vec{i}+x_2\vec{j}+x_3\vec{k}$ is also used in some calculations but notice that this notation has no immediate generalization to higher dimensions. However it is sometimes helpful in telling the difference between a point and a vector. In calculations we don't need this distinction so I will stick with the point notation.
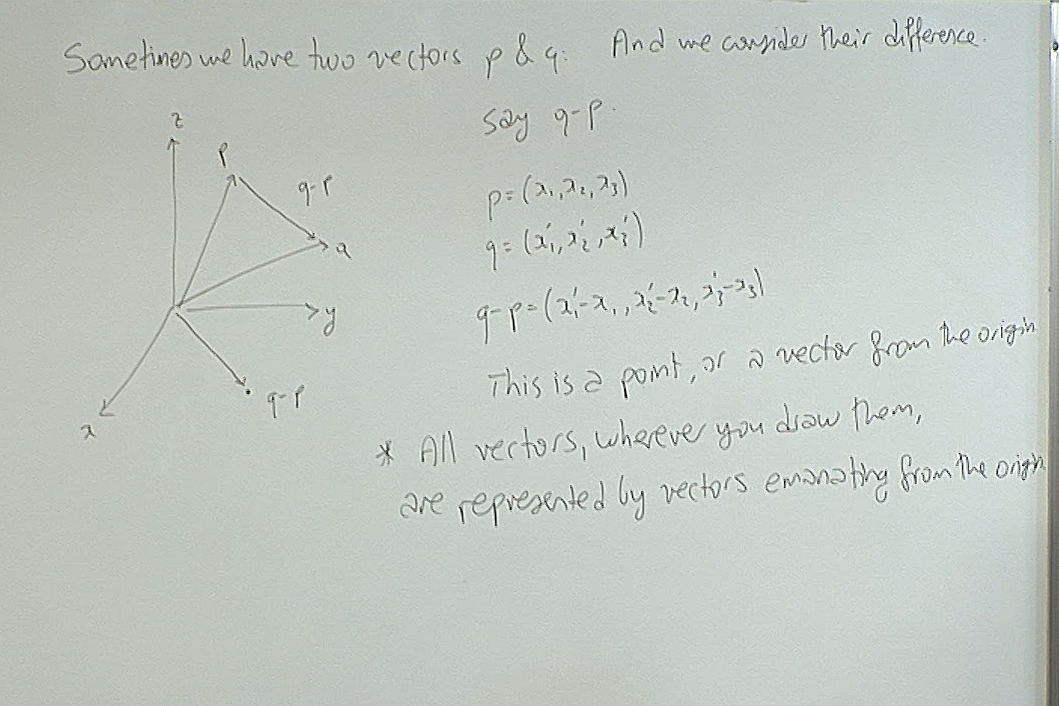
The important message here is that even though we like to draw vectors at geometrically significant places in our figures, algebraically all vectors behave as if they are emanating from the origin. In other words, all vectors behave as if they are points in space given by the usual notation $p=(x_1,x_2,x_3)$.
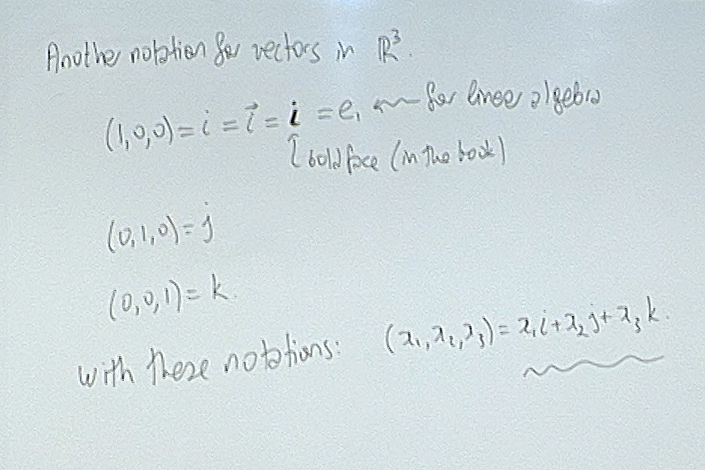
This notation, though convenient in $\mathbb{R}^3$, does not allow our intuition to adopt to higher dimensions, so I will use it sparingly.

The short hand "s.t." above stands for "such that" and is widely used by teachers around the world!
Here we are starting to relate geometry with algebra; how to describe algebraically a region we 'see' in space and conversely how to 'see' the region that is described by some algebraic expressions. Some practice is needed.
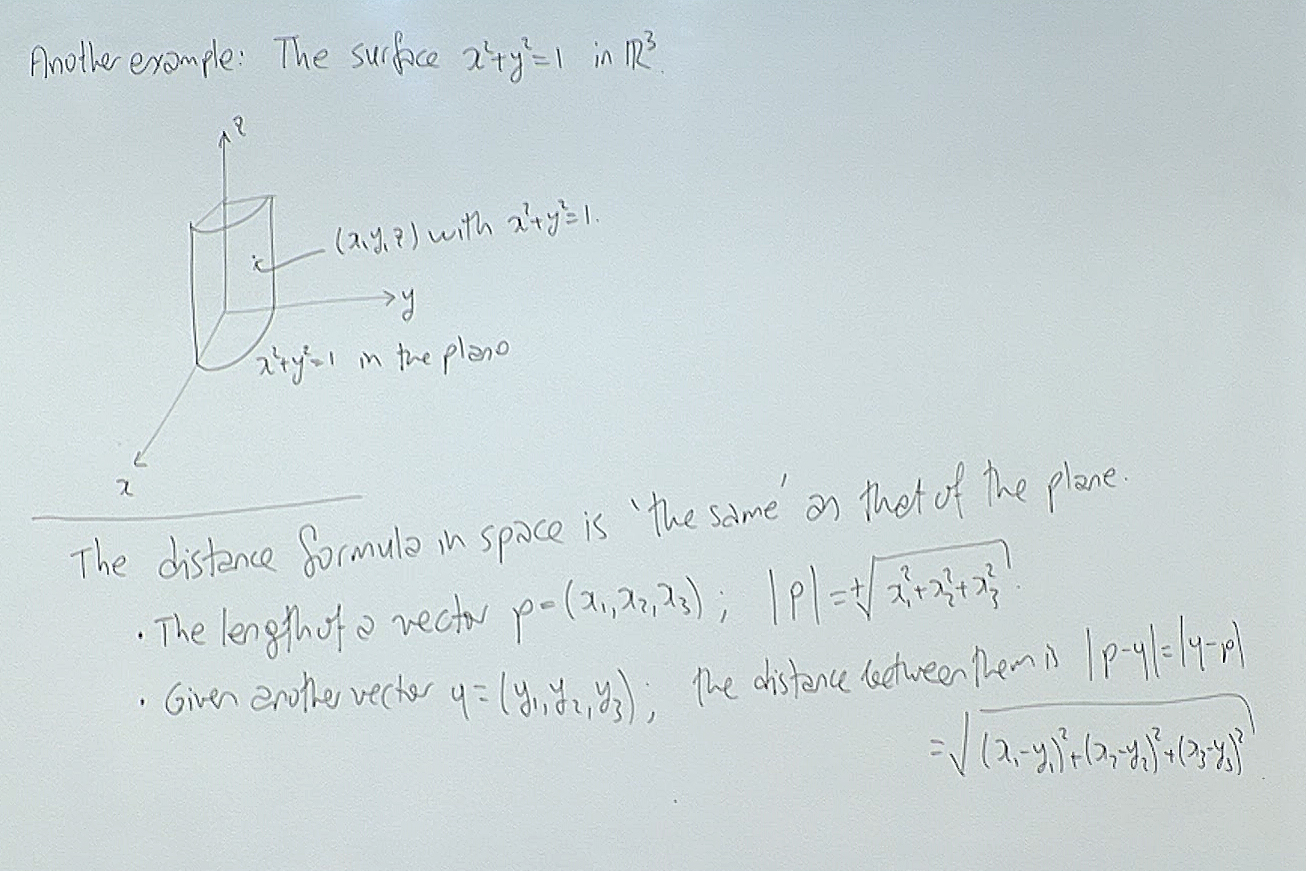
The surface defined at the top is an example of a "cylindrical surface". Here a relation between the $x$ and $y$ coordinates is given. Any point of the form $(x,y,z)$ is on this surface as long as the $x$ and $y$ satisfy the given relation. The $z$ coordinate is left free to tak any value.
The distance function, as you notice, is the extension into space of the usual Pythagoras theorem for the length of the hypothenuse of a right triangle.

In particular if the center is the origin, then $x^2+y^2+z^2=R^2$ is the equation of the sphere. In most cases we arrange our coordinates so that the center of the sphere will be at the origin for ease of calculation.

In short, vectors can be added and subtracted. Also vectors can be multiplied by scalars. All these are coordinate wise operations.
Notice that we are not attempting to multiply vectors by vectors. That is a very long story. We will use a special vector product for $\mathbb{R}^3$, but other than that vectors will not be multiplied by each other to give another vector.
