Previous Screenshot Next Screenshot

Notice that by using the dot product we are multiplying two vectors but we are not obtaining another vector as a result; we are obtaining a real number instead. This number has some geometric significance as we will see shortly.
The dot product is a very special case of what is called an inner product in Linear Algebra which you will probably take next year. When the entries of the above matrix are all integers, then this inner product is a subject of Number Theory which you may take as an elective course later.
For now just notice how easy it is to calculate the dot product of two vectors once their entries are known.

We use $0$ to denote the real number $0$ as well as the zero vector in any space. This abuse of notation does not cause any problem since it is always clear from the context what we mean.

This is the reason why we use the dot product. It is very easy to calculate but it has a geometric message encoded to it; the angle between the two vectors. We are mostly interested if this angle is $90^\circ$ or not. If that angle is $90^\circ$, then notice that the dot product is zero since $\cos 90^\circ=0$.

This is another geometric information encoded into the dot product. We can write $\vec{b}$ as the sum of two vectors, one along $\vec{a}$ and the other perpendicular to $\vec{a}$. To see how this is possible, let \[ \vec{u} = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|^2}\; \vec{a}, \; \; \; \vec{v}=\vec{b}-\vec{u}. \] Now check easily that\[ \vec{b}=\vec{u}+\vec{v}, \; \; \text{and} \; \; \vec{u}\cdot\vec{v}=0. \]

The term "orthogonal" is generally used to mean that eiher the vectors are non-zero and perpendicular to each other or at least one of them is the zero vector. In short "orthogonal" means that the dot product of the two vectors are zero and we don't have time to check if the vectors are non-zero or not!

Most of the time we use this to compare the sizes of the angles between several vectors rather than actually finding out what the angles are.

The abbreviation "iff" is another short hand mathematicians use in informal writing: it means "if and only if".
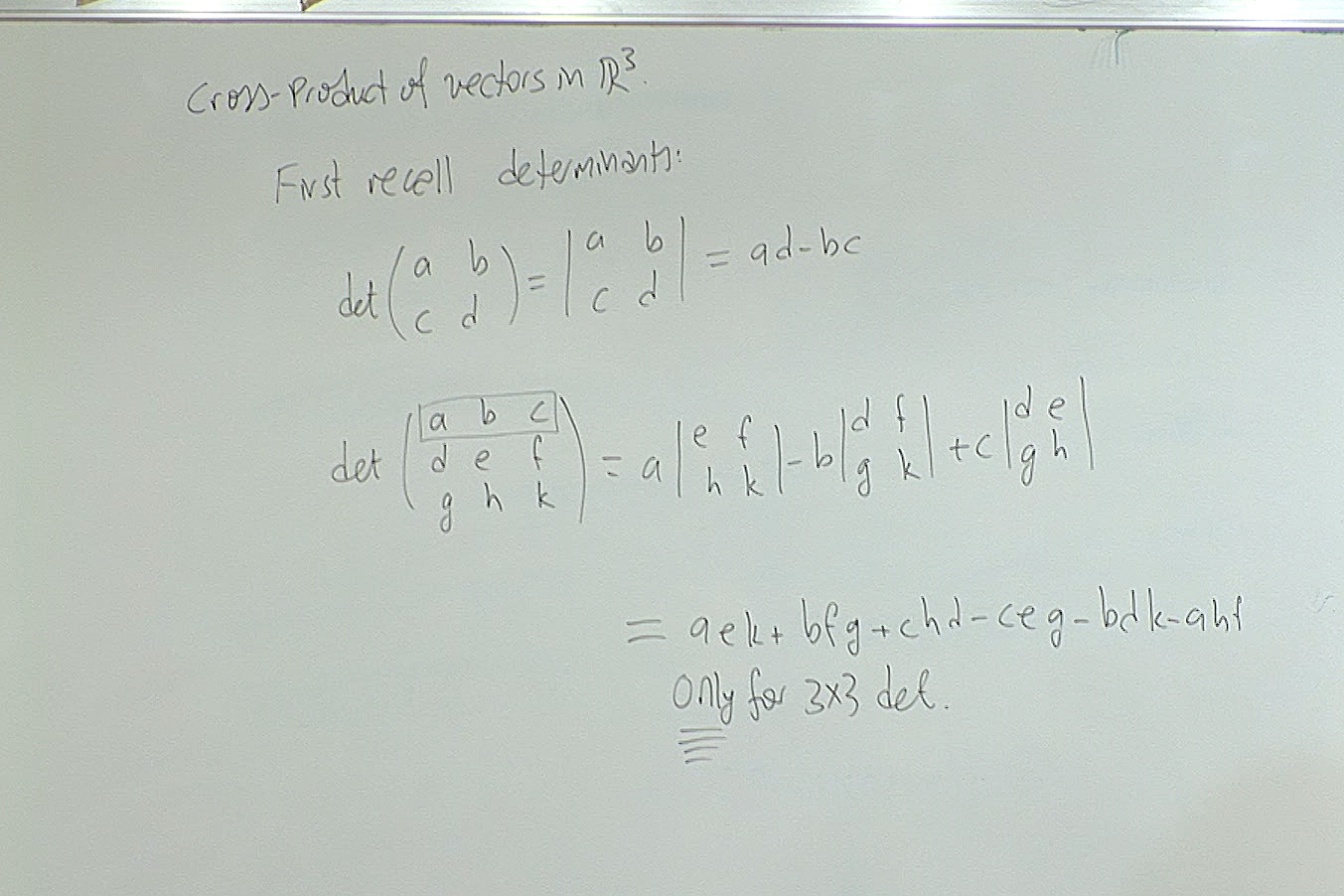
We will use this particular expression of determinant for $3\times 3$-matrices. In particular if you check the expression of the determinant in the middle of the above screenshot, you will see that it still makes sense if we replace $a,b,c$ by vectors! It then becomes a sum of vectors. We will exploit this in the next screenshot.

Here "formal determinant" means calculate the determinant using the given symbols without asking questions! When you do that you obtain a vector. This way we managed to multiply two vectors in $\mathbb{R}^3$ and obtain another vector again in $\mathbb{R}^3$. Notice that this particular way of multiplying two vectors to obtain another vector of the same dimension works only in $\mathbb{R}^3$.
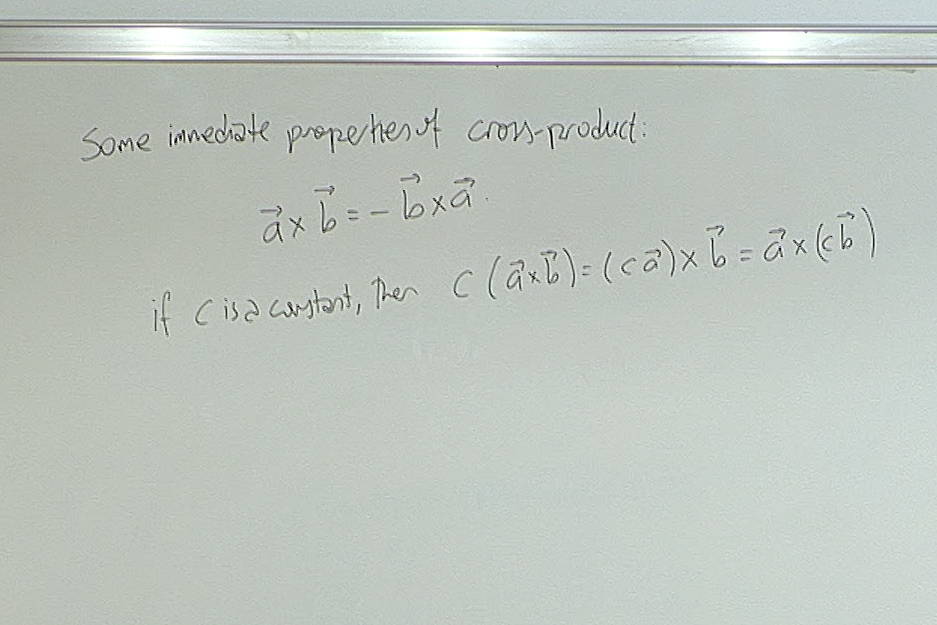
There are two basic properties of this product, the cross-product, that we should keep in mind. First it is anti-commutative; if you change the order of multiplication, you change the sign. The other important point to keep in mind is that no division is possible.
In other words, if you take two vectors $\vec{a}$ and $\vec{c}$, you will find out that either there are infinitely many vectors $\vec{b}$ such that $\vec{a}\times\vec{b}=\vec{c}$ or none at all. Try it!
The other properties of the cross-product are technical and can be looked up from a book when needed.