
Previous Screenshot Next Screenshot

The dot product takes two vectors, in any dimension, and gives a number. Let \[ \vec{u}=(a_1,\dots,a_n)\in\mathbb{R}^n, \; \; \text{and} \; \; \vec{v}=(b_1,\dots,b_n)\in\mathbb{R}^n. \] Then \[ \vec{u}\cdot\vec{v}=a_1b_1+\cdots+a_nb_n\in\mathbb{R}. \] The formula \[ \vec{u}\cdot\vec{v}=|\vec{u}|\, |\vec{v}|\, \cos\theta \] is still valid as explained in the above screenshot.

Note that here we need the absolute value of the determinant to find the area since changing the order of the vectors certainly does not change the paralellogram but the determinant changes sign.
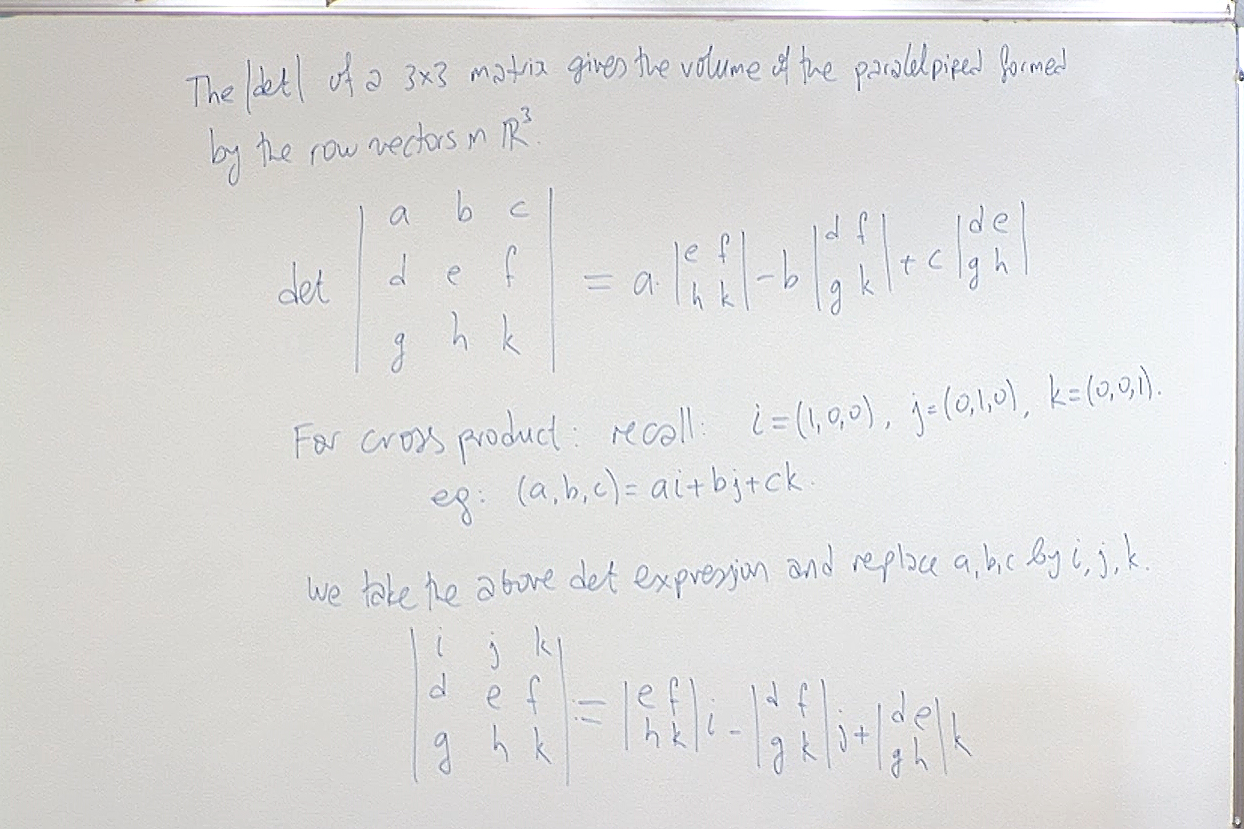
The geometric description of the (absolute value of the) determinant as area is useful; if the first row is the same as the second row (or the thırd row), then those three rows generate only a parallelogram not a parallelepiped, so the volume must be zero. We will use this observation shortly.
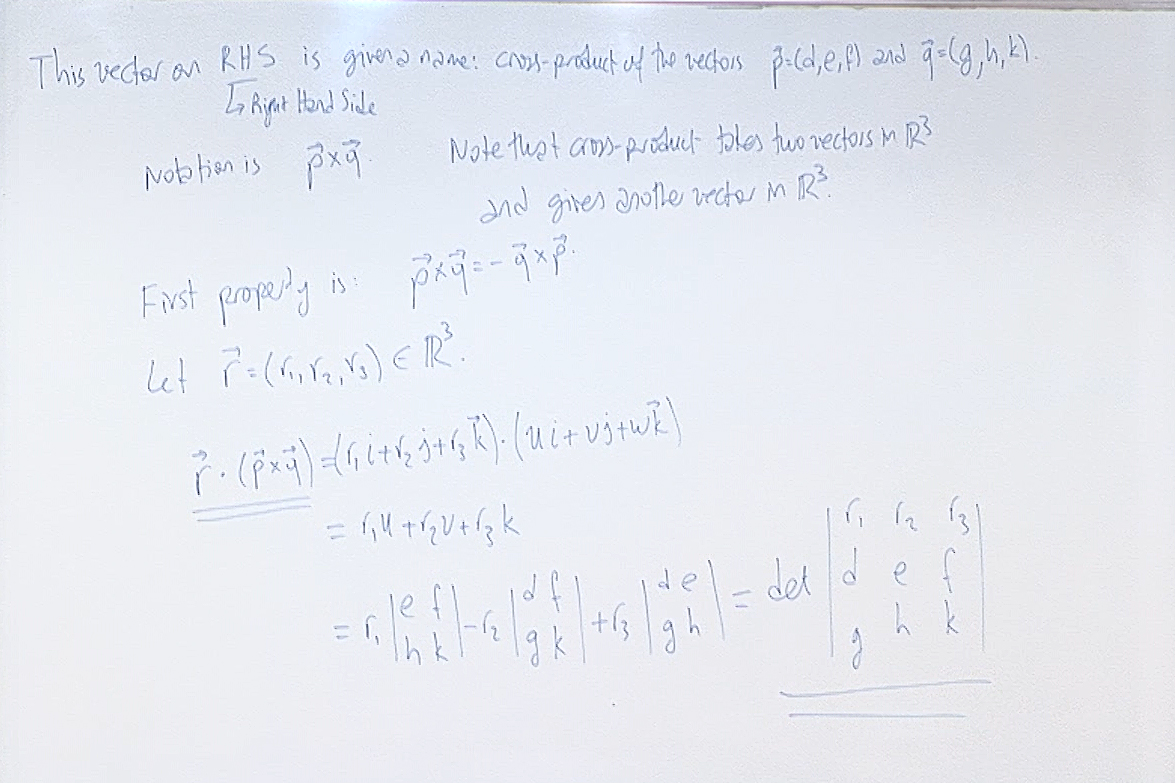
We calculate the dot product of $\vec{p}\times\vec{q}$ with an arbitrary vector $\vec{r}$ as a preparation to understand towards which direction the cross-product points.

The observation that $\vec{p}\times\vec{q}$ is orthogonal to the plane in which $\vec{p}$ and $\vec{q}$ lies is probably the main reason why we use cross-product.


You have to remember how to calculate the dot product and the cross-product and also keep in mind the properties listed above as "Summary". This is all we need later.

This is a numerical example to convince you that the cross-product is anti-commutative, i.e. $\vec{q}\times\vec{p}=-\vec{p}\times\vec{q}$.

A numerical problem to show how geometry and algebra work together.
