
Previous Screenshot Next Screenshot
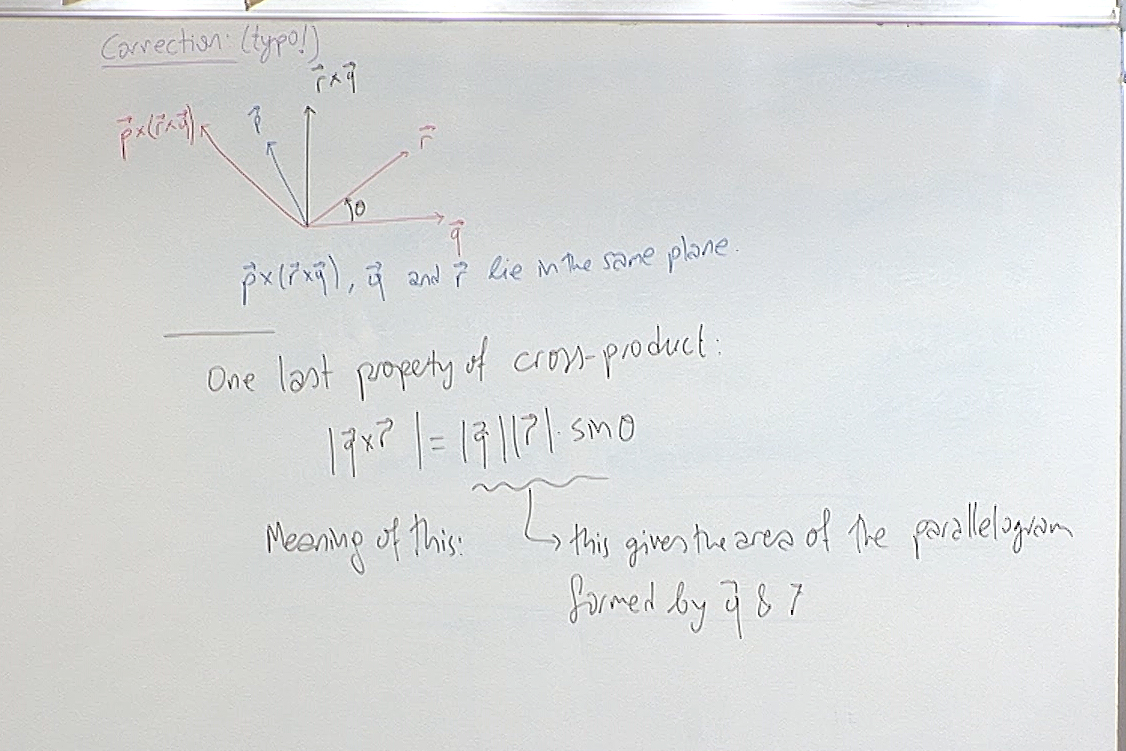
The correction mentioned at the top was on the 6th screenshot of the previous hour and has already been corrected on that screenshot.
The property mentioned at the bottom is sometimes useful so it is worth to keep it in mind.

A single linear equation in the plane describes a line. However in higher dimensions such as in $\mathbb{R}^n$, a single linear equation describes an $n-1$ dimensional linear subspace and this linear subspace is a line only when $n-1=1$, i.e. when $n=2$. So we need to be familiar with vector description of a line, which works in any dimension.
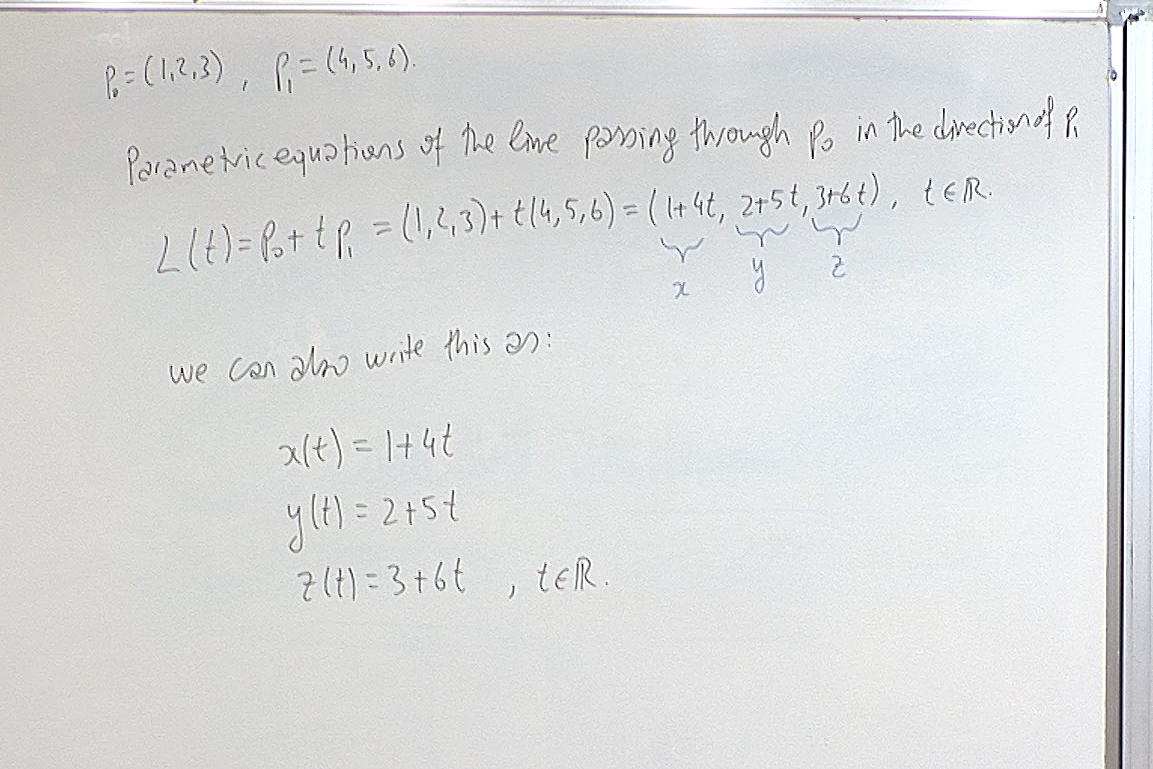
The $L(t)$ expression is called the vector notation, and the last three equations are called the parametric equations of the line.

The symmetric equations are useful when we want to see the planes in which the line lies. The numbers in the denominators give the direction of the line.
If the direction vector contains a zero, then the symmetric equations break up as follows. For example if the line passes through the point $(a,b,c)$ and is parallel to the vector $(0,B,C)$, then the symmetric equations are written as\[ x=a, \; \; \frac{y-b}{B}=\frac{z-c}{C}, \] assuming $BC\not=0$.
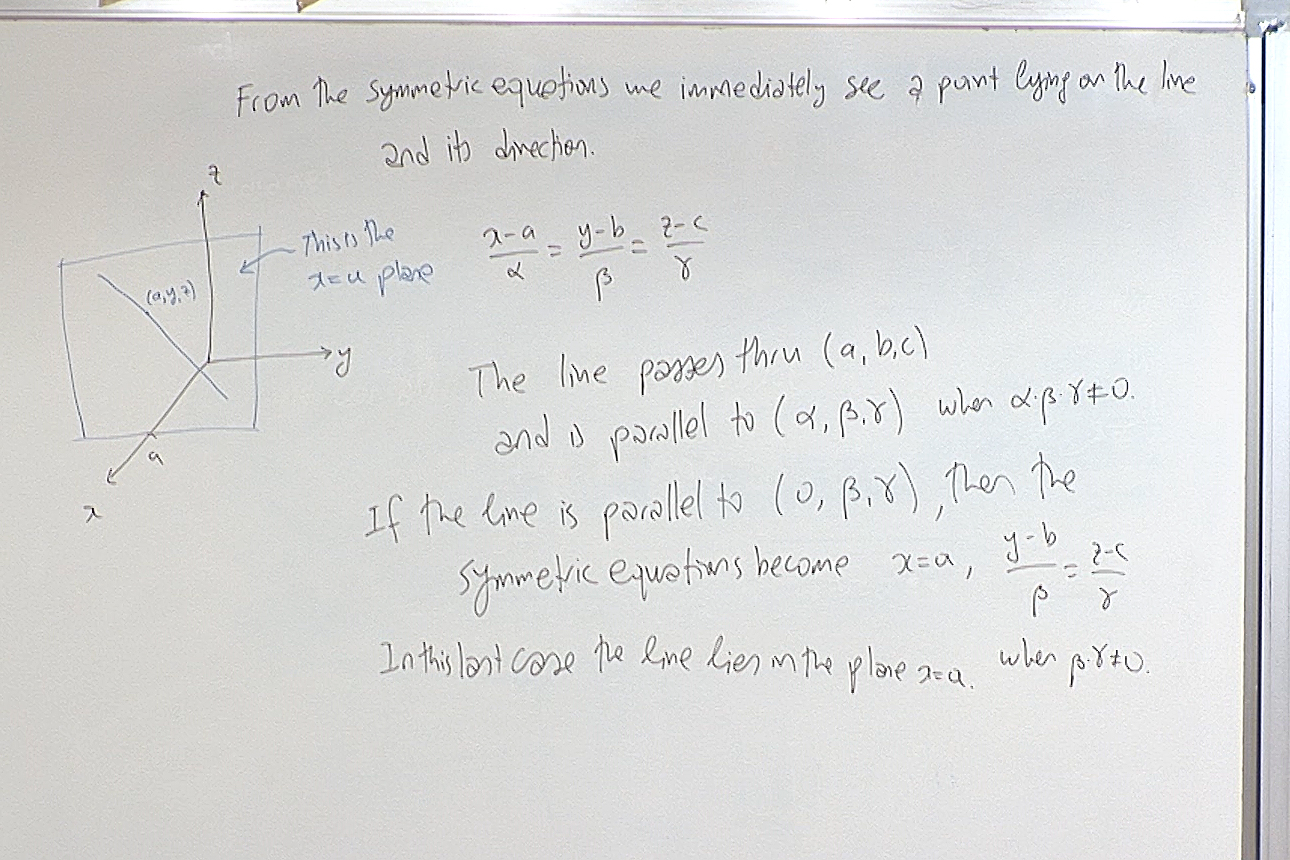
In the above example, if further $\beta$ is also zero, the symmetric equations become \[ x=a, \; y=b. \] The line is now the intersection of the above two planes. Since the $x$ and $y$ coordinate are fixed, the $z$ coordinate is free and there is no need to mention that $z=c+t\gamma$.

The above $P(s,t)$ is a parametric equation of the plane and works in any dimension.

This is the geometric description of the line and its algebraic expression is also easy to write. Once $(p-p_0)\cdot \vec{n}=0$ is simplified it becomes \[ A(x-a)+B(y-b)+C(z-c)=0, \] or \[ Ax+By+Cz=Aa+Bb+Cc. \] Here $\vec{n}=(A,B,C)$ is an orthogonal vector to the plane, and this last equation says that every point on the plane must have the same dot product value with the normal.
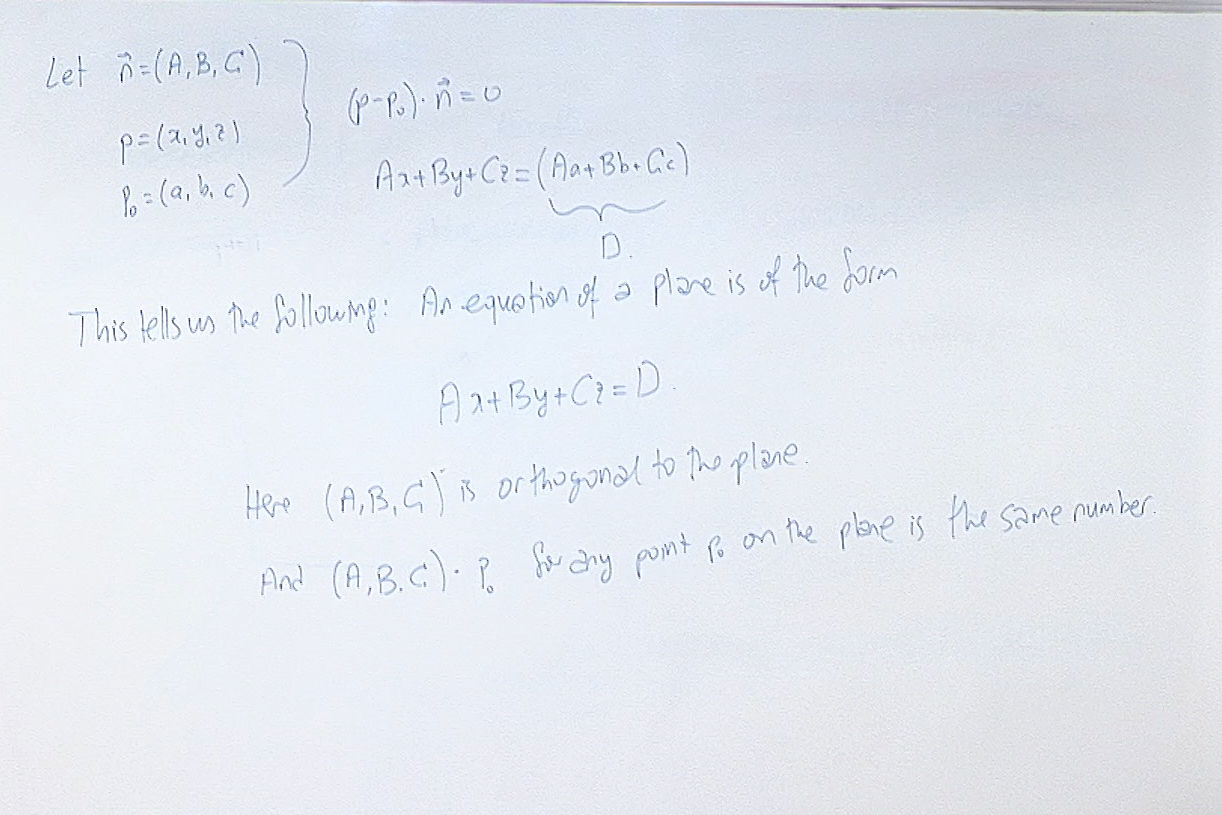
Here we read information about the plane from its equation $Ax+By+Cz=D$.

The crucial step here is to calculate a normal vector $\vec{n}$. Here the order of the points $p_1,p_2,p_3$ is not important. You can shuffle them in any way you like, fix one of them and take its difference from the remaining two, and calculate the cross-product of those two differences as we did above. Call this cross-product $\vec{n}$. Then an equation of the plane is \[ \vec{n}\cdot (x,y,z)=\vec{n}\cdot q, \] where you can take $q$ to be any of $p_1,p_2,p_3$.
