

The two methods mentioned here demonstrate the theory behind the set up. In 'real life' you simply consider the vectors \[ B-A=(1,3,-4) \; \text{and} \; C-A=(-1,-1,-1), \] and check if one of them is a constant multiple of the other. Here it is clear that $B-A$ does not point in the direction of $C-A$, so these three points $A$, $B$ and $C$ are not collinear.

The above determinant calculates the volume of the parallelepiped formed by these three vectors and the origin. If the points $A$, $B$ and $C$ lie along a line (collinear), then they are in the same plane (coplanar). Then they cannot form a three dimensional parallelepiped with positive volume. Here the determinant shows that they form a parallelepiped with a positive volume so they don't lie in the same plane. Thus they have no chance of being collinear.
Let me repeat that three points $A,B,C$ are colliner if and only if we can multiply $B-A$ by a constant and obtain $C-A$. In this case there is no $\lambda$ to achieve this since \[ B-A=(1,3,-4) \; \text{and} \; C-A=(-1,-1,-1). \] Note that the ordering $A,B,C$ is not important. You can choose them in any order.
Incidentally, the area of the parallelogram defined by $B-A$ and $C-A$ is $|(B-A)\times (C-A)|=78$. This again says that these points are not collinear.

Here $B-A=(1,3,-1) $ and $C-A=(3,9,-3)$, since $3(B-A)=C-A$, the vectors $A,B,C$ are collinear.


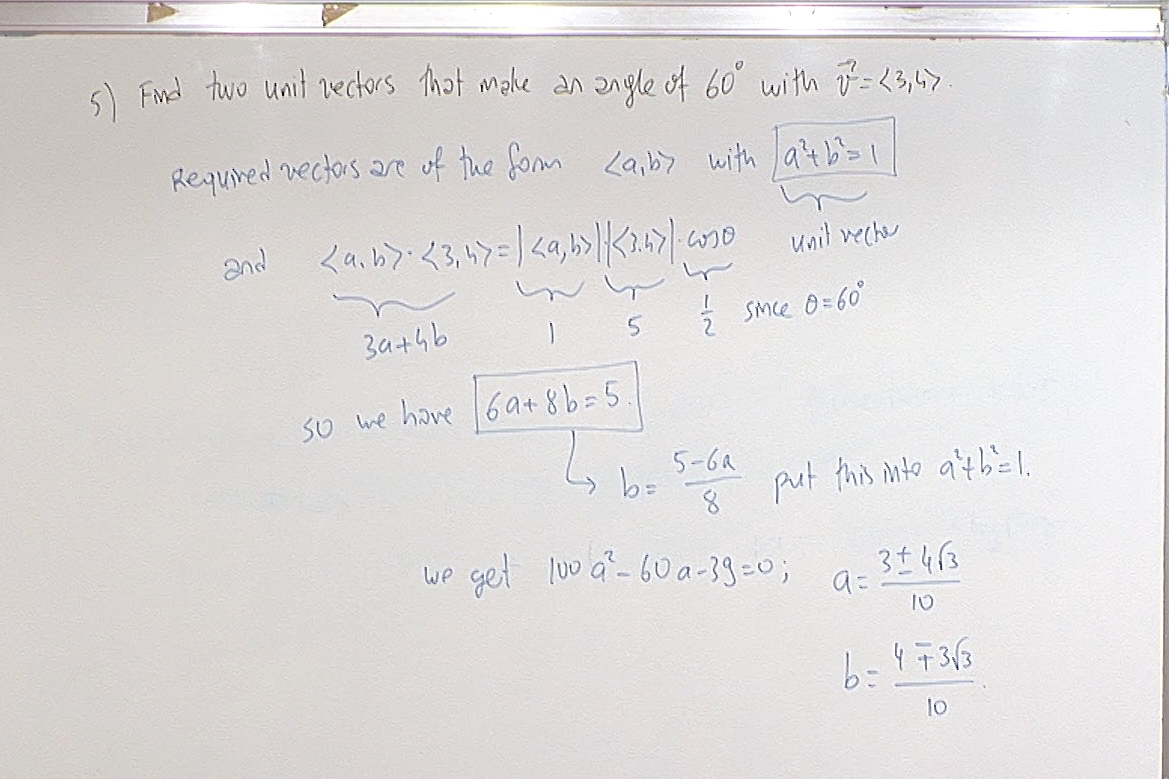
So the required vectors are $\displaystyle \frac{3+4\sqrt{3}}{10}\, \vec{i}+ \frac{4-3\sqrt{3}}{10}\,\vec{j}$ and $\displaystyle \frac{3-4\sqrt{3}}{10}\, \vec{i}+ \frac{4+3\sqrt{3}}{10}\,\vec{j}$.
Notice that in the above screenshot I suddenly started to use $\langle a,b\rangle$ to denote $(a,b)$. We can also use $a\, \vec{i}+ b\, \vec{j}$. Don't get confused.

Recall that the symmetric equations are obtained by simply eliminating $t$ from the parametric equations.

