

We need to parameterize curves because later we will restrict a function on a curve and examine its behaviour along that curve.

Here is how a cycloid is drawn in general:

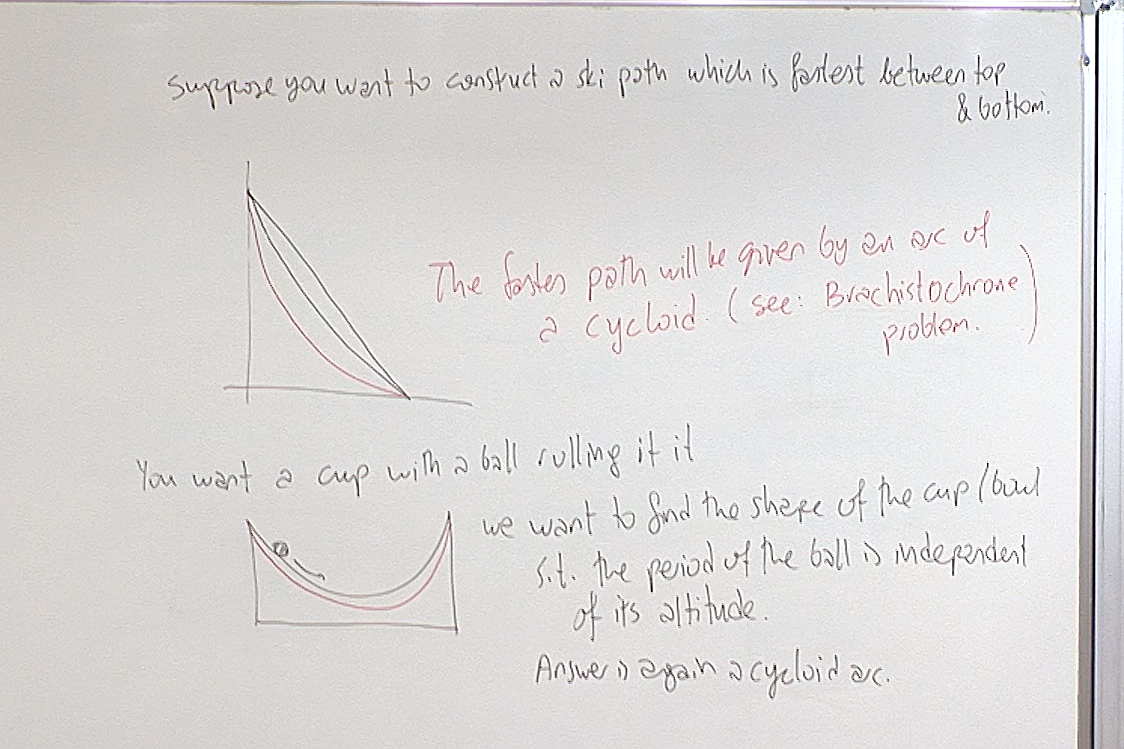
The first problem is known as the Brachistochrone problem: see Wikipedia article.
The second problem is known as the Tautochrone problem: see Wikipedia article.

One amazing thing about curves is that if you pick a general point on it and magnify the picture a few hundred times, or more, you will eventually start seeing almost a straight line. For example if you look around now, you will think that the Earth is flat, i.e. it is like a plane. This is the fundamental observation at the heart of geometry. Geometric objects generally look like $\mathbb{R}^n$ locally. If a particular point on the geometric object fails to convey this sense of being 'flat', that point is called a singular point. "Singular" is polite for "bad".
For example the point $(0,0)$ on the curve $y^2=x^3$ is a singular point.

In any dimension, if $\vec{r}(t)$ is the position vector for a curve, then $\displaystyle \frac{\partial \vec{r}(t)}{\partial t}=\vec{v}(t)$ is the velocity vector. The velocity vector is tangent to the curve at the point $\vec{r}(t)$ and points in the direction of motion of a particle on the curve. We are of course doing all this with the assumption that each entry of the position vector is a differentiable function of $t$.
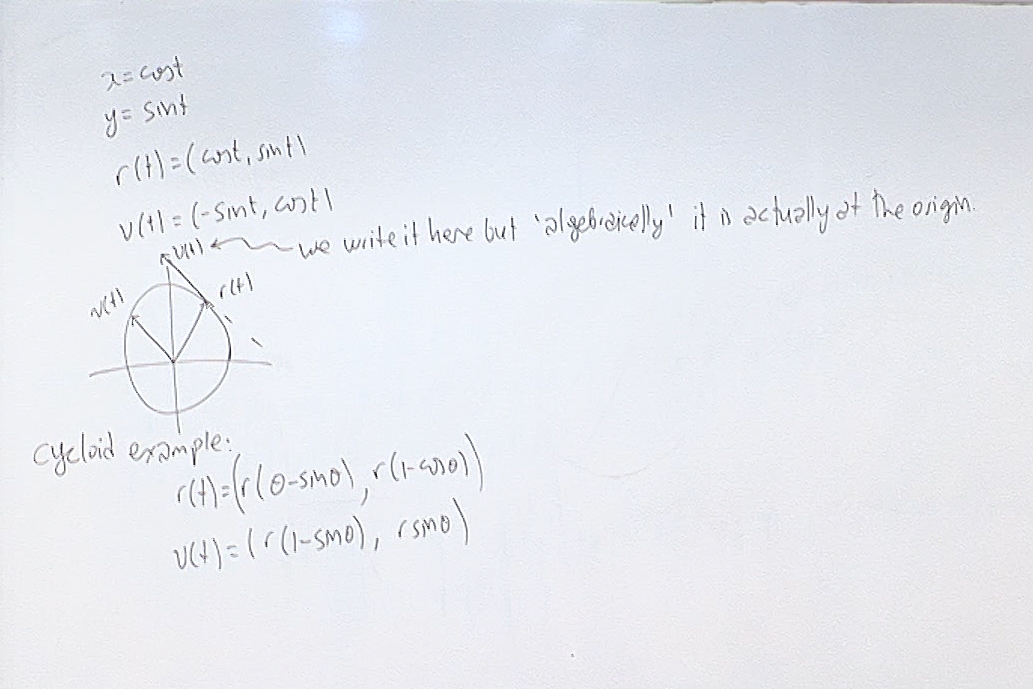
We draw a vector where it makes sense for us but while doing calculations with it we must remember that all vectors emanate from the origin.

We use this when the slope of a parametric curve is required. Note that if $\displaystyle \frac{\partial x}{\partial t}=0$, then the tangent vector is vertical so it has no algebraic slope.


