

Most of these are reminders so you can skip over them quickly. On the right bottom $|\vec{a}\cdot(\vec{b}\times\vec{c})|$ is of course the volume of the parallelepiped formed by those vectors.


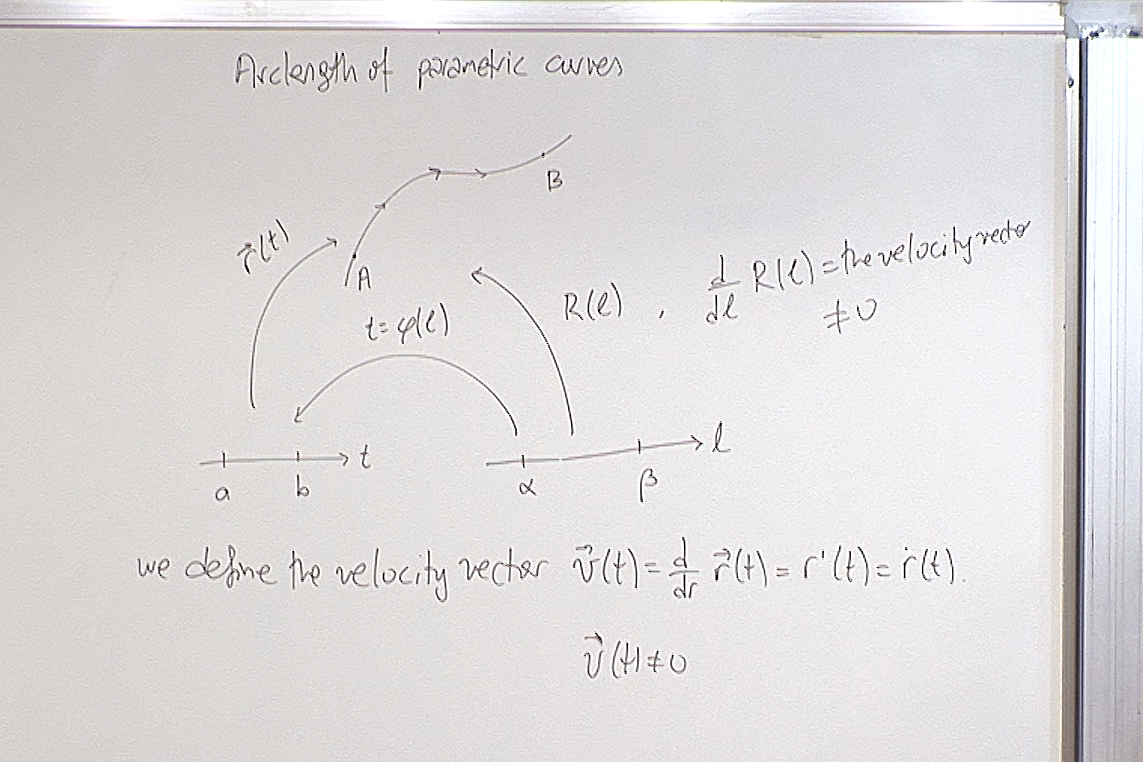
Here we consider two different parametrizations of the same curve. We will show that the arclength of the curve can be calculated by using either parametrization. What we require from a parametrization is that its velocity vector never vanishes, except may be at the end points. This guarantees that the parametrization is actually one-to-one as we would expect from a parametrization.

At the end we change from $t$ to $\tau$ as a notational convenience since sometimes we want to evaluate the integral up to an arbitrary $t$ instead of a fixed $b$. Then the two $t$, one appearing in the limit of the integral, the other in the integrand can be confusing.

This is where we establish the fact that whichever parametrization you use for a curve, integrating its velocity vector will give the arclength. This is all you have to remember in the calculations.
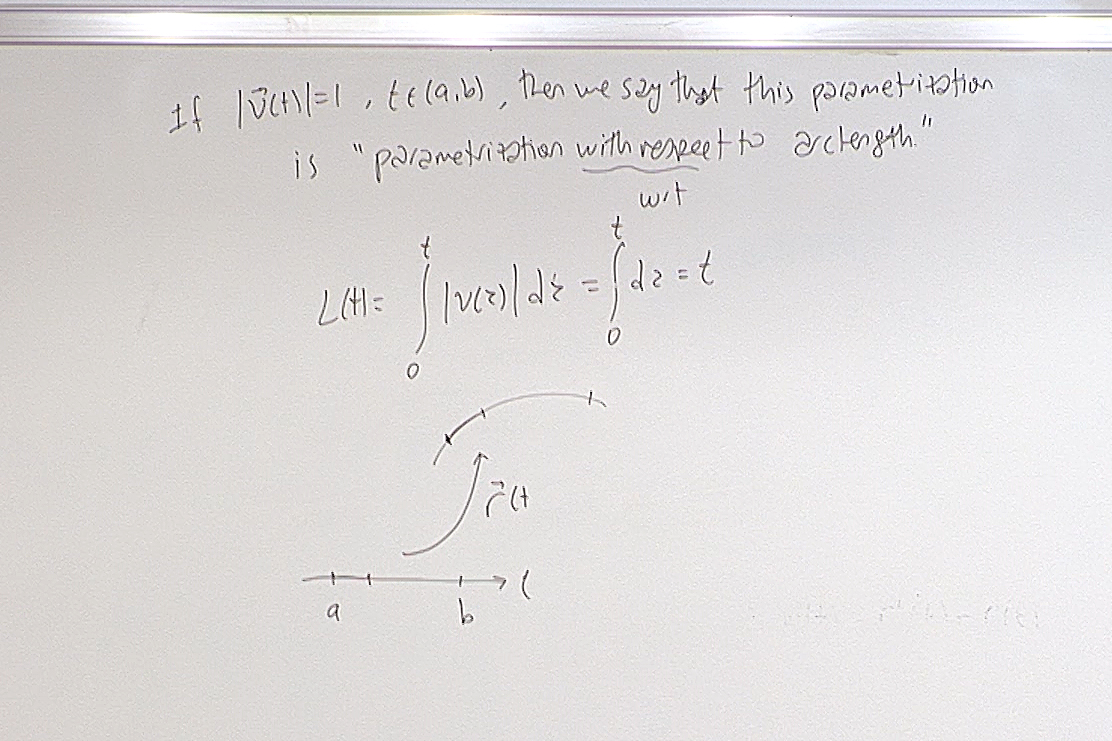
We mention this terminology since it is widely referred to but we will not be using it.
At this point we had a quiz. Here is the question.

