
Previous Screenshot Next Screenshot

Even though in Calculus II we deal with only 2 or 3 variables, the techniques that we will develop will work for more than 3 variables too. But it is impossible to draw reasonable pictures in higher dimensions we we decide to stop at 3 dimensions in Calculus.

Domain is important and most of the time easy to detect. Range is more complicated to determine since you have to solve equations. We generally do not mention the range unless it is obvious.
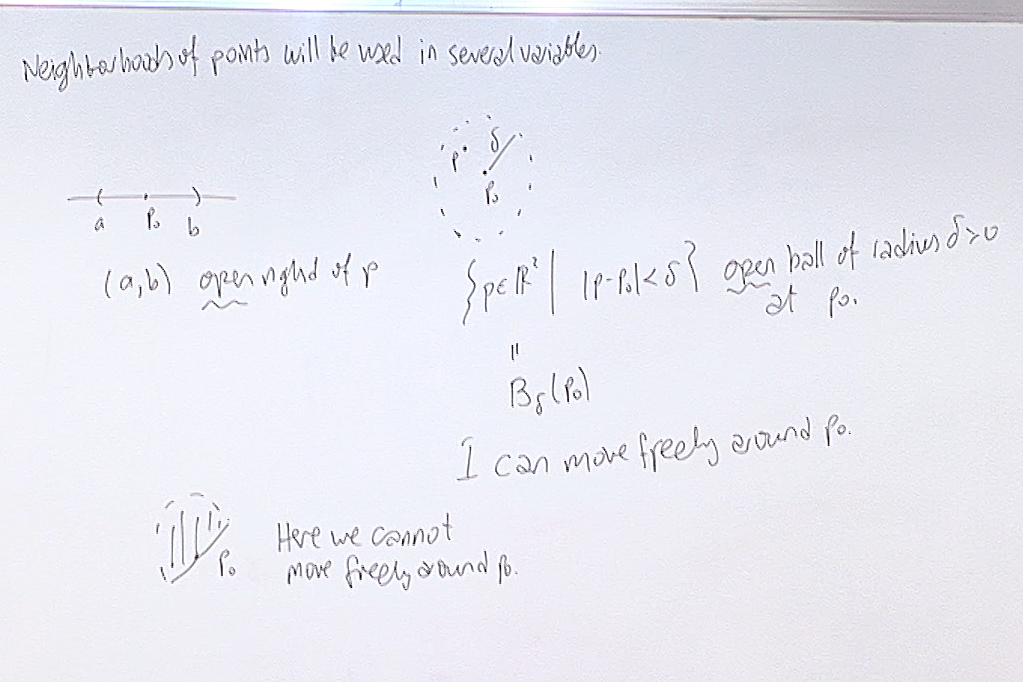
This is the crucial part of several variable theory. Whereas you can approach a point from only right or left on a line, in the plane there is no specified or distinguishd manner of approach to a point. What matters here is whether you are close to a point or not.

The closeness will be determined by the topological concept of an open set.

The words "open" and "closed" are opposite of each other in everyday speech but as mathematical terms they are not. A set can be both open and closed. For example the whole plane is both an open subset and a closed subset of the plane! Also a set can be neither open nor closed. Just take an open ball and add one point of its boundary to the ball. The resulting set is now neither open nor closed.
But we will not be going into details of these topological concepts. We will work on open sets and sometimes we will talk about their boundary points. That is all we need.

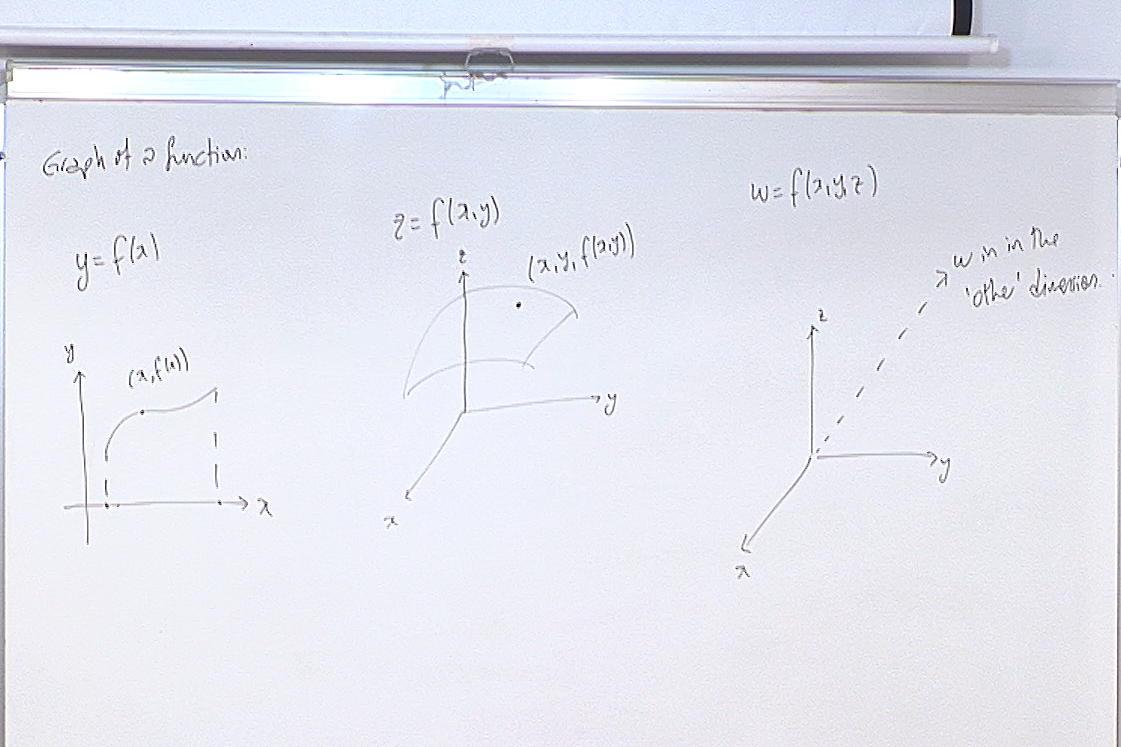
The "picture" on the right explains why we stop at 3 dimensions in Calculus. The $w$-axis must be perpendicular to all the other axes. This cannot be visualized in 3 dimensions. However our techniques will let us 'guess' what is happening in higher dimensions without trying to draw a picture.
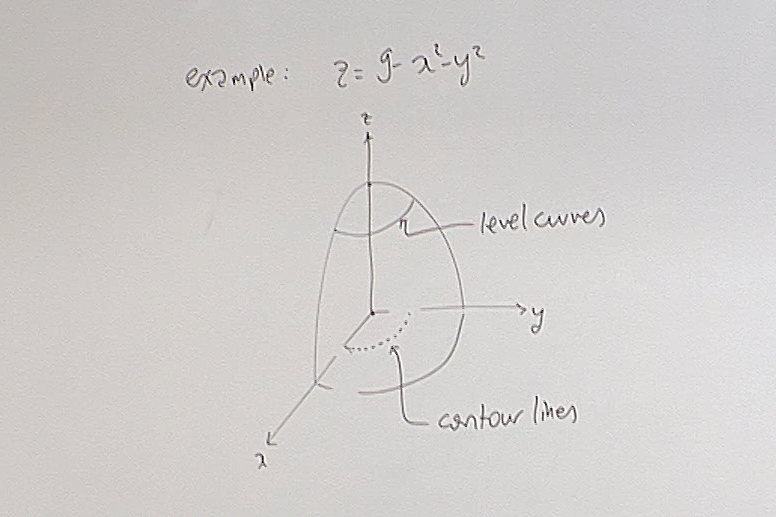
The terms "level curves" and "contour lines" are not universally fixed. If you are using a book, check what your author is using. In this terminology, level curves are the points on the surface which have the same $z$ value, and contour lines are the points in the domain which give the same $z$-values. Here the surface is understood to be given as $z=f(x,y)$.

This is the formal definition of limit but we seldom use the formal definition. The meaning of this definition in everyday parlance is the following. When we say \[ \lim_{p\rightarrow p_0}f(p)=L, \] we mean that the values of $f(p)$ are getting closer to the value $L$ as the point $p$ is getting closer to $p_0$. But how close is close enough? We say you decide what size of $|f(p)-L|$ will make you happy. Then I will find an open ball $U$ around $p_0$ so that whichever point $p$ you pick from the ball $U$, you will have the size of $|f(p)-L|$ small enouh to make you happy.
Now read the formal definition with this in mind. There, anything smaller than $\epsilon$ will make you happy, and $\delta$ is the radius of the open ball $U$ which I promised to you.
