
Previous Screenshot Next Screenshot
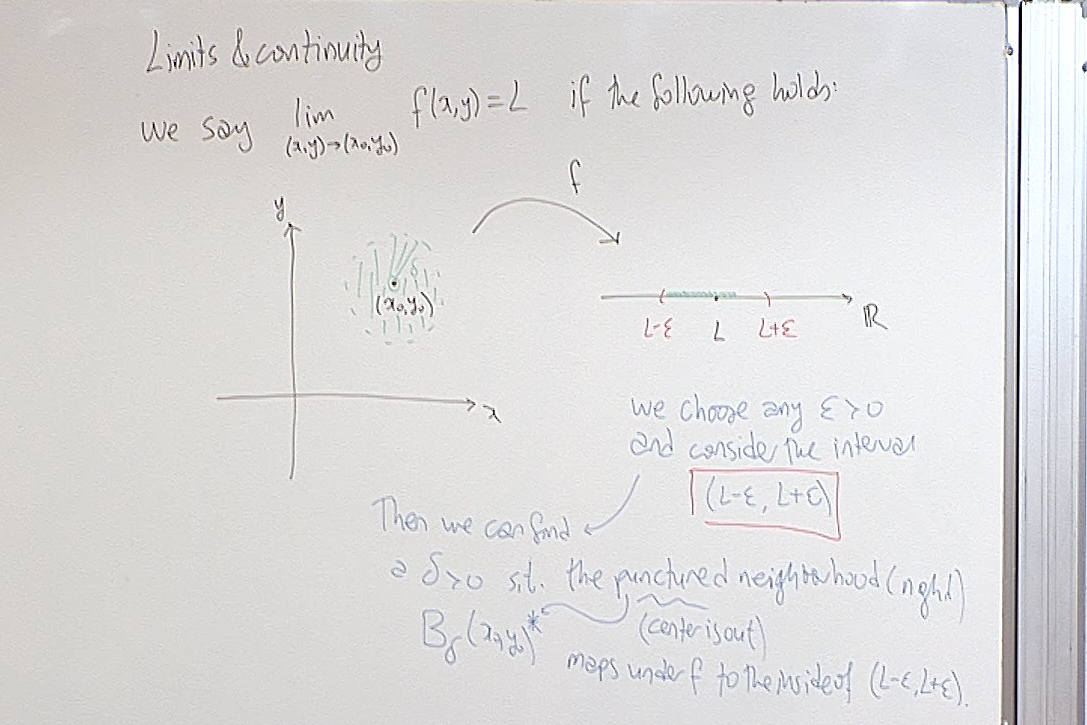
Here recall that \[ B_{\delta}(x_0,y_0)=\{ (x,y)\in\mathbb{R}^2 | (x-x_0)^2+(y-y_0)^2 < \delta^2 \}, \] and $B_{\delta}(x_0,y_0)^\ast$ means that you take out the center of the ball, \[ B_{\delta}(x_0,y_0)^\ast=\{ (x,y)\in\mathbb{R}^2 | 0<(x-x_0)^2+(y-y_0)^2 < \delta^2 \} . \] What is important here is to observe that there is no prefered way of approach to $(x_0,y_0)$ in the plane. So we use the concept of "being close to $(x_0,y_0)$", and this concept is implemented as follows: instead of saying that "$(x,y)$ is close to $(x_0,y_0)$", you choose a $\delta>0$ and say that "$(x,y)$ is in the ball $B_{\delta}(x_0,y_0)$." If you want to be closer, you choose a smaller $\delta>0$.

This basically says that you can first calculate the limits of the small pieces and then put the limits back together the same way the pieces were put together.

Just as in the one variable case, a function is continuous if it commutes with the limit operation. We recognize that polynomials, trigonometric functions and rational functions are continuous in their domains. Moreover composition of continuous functions are continuous.

If the limit exists without putting imposing any special pattern of approach on $p$, as $p\rightarrow p_0$, then all limits where you choose to impose any convenient pattern of approach you like on $p$ will give the same limit. This is obvious but it helps us to determine when the limit does not exist, as we will see in the next screenshot!

If you calculate the limit along two special paths and obtain two different limits, then the actual limit, where we let $p\rightarrow p_0$ without any restriction, does not exist. This is known as the Two Path Test for Divergence.
The second theorem mentioned above is the Sandwich Theorem, which we sometimes also call the Squeeze Theorem.
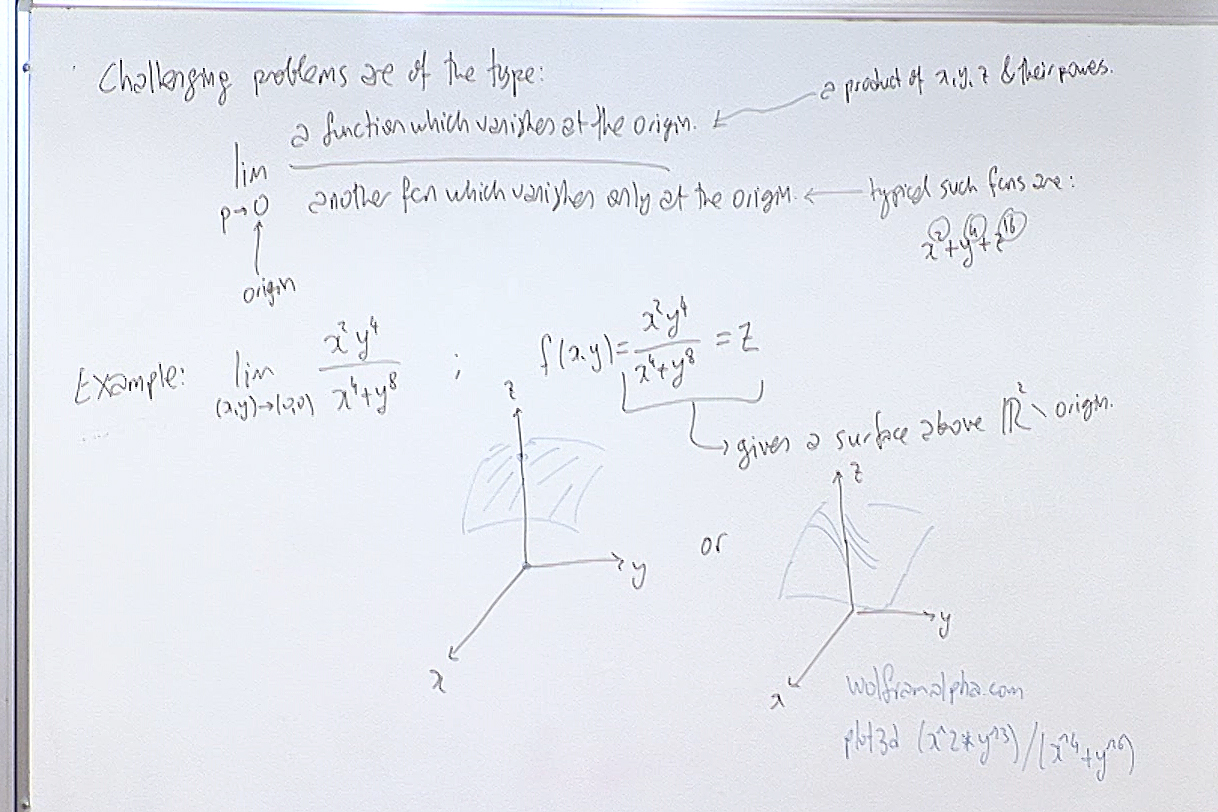
The limits of the above type of rational functions at the origin appear very often. As a warm up I recommend that you visit this page first!

This is an application of the Two Path Theorem for Divergence. When $p$ approaches the origin along different paths, the limit changes according to the line of approach. Hence the limit does not exist.
