
Previous Screenshot Next Screenshot
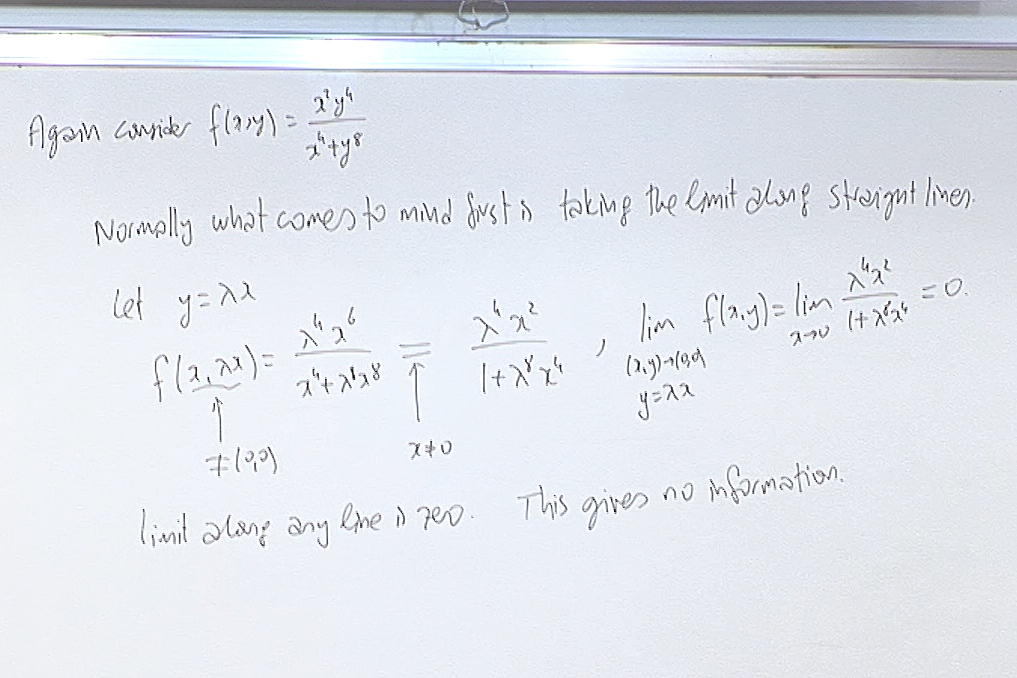
Here try the path $x=\lambda y^2$. You will have \[ \lim_{(\lambda y^2,y)\rightarrow (0,0)} \frac{(\lambda y^2)^2y^4}{(\lambda y^2)^4+y^8} 0 \lim_{y\rightarrow 0}\frac{\lambda^2 y^8}{\lambda^4y^8+y^8}=\lim_{y\rightarrow 0}\frac{\lambda^2 }{\lambda^4+1}==\frac{\lambda^2 }{\lambda^4+1}, \] and you see that the limit depends on the path. So the limit does not exist. We will see in a minute an easier way of reaching to the same conclusion.
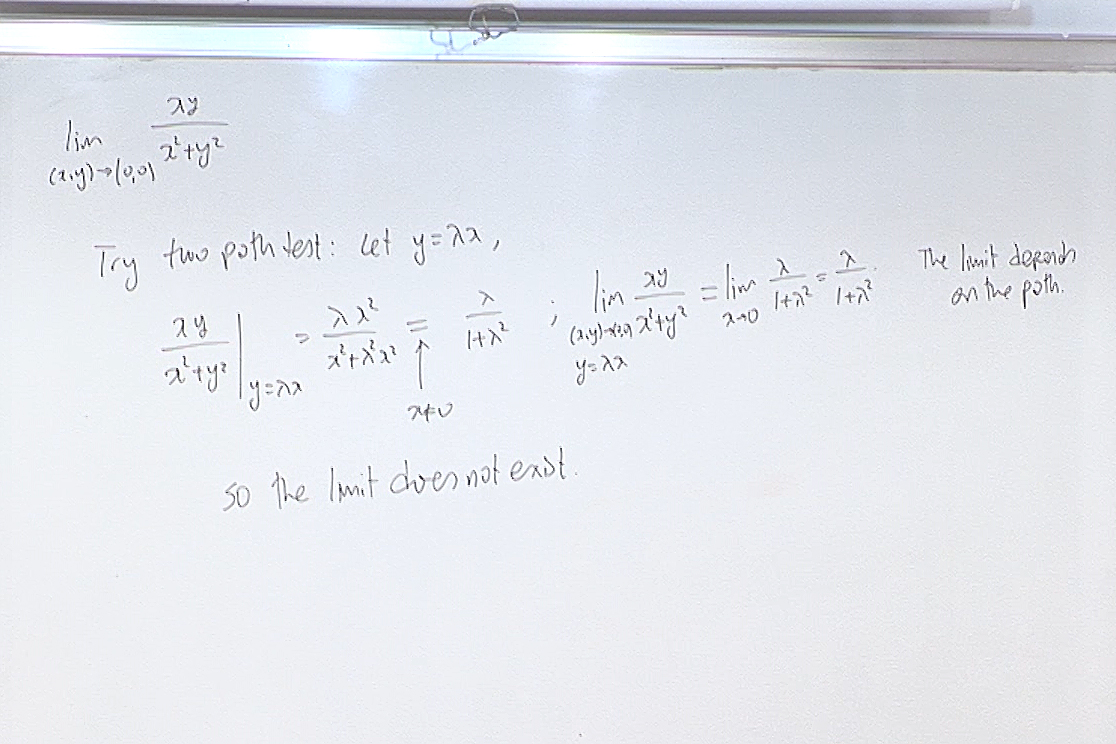
Here the Two Path test for Divergence gives the result in one step.

When the exponents of the numerator are large, we can use the Squeeze Theorem.
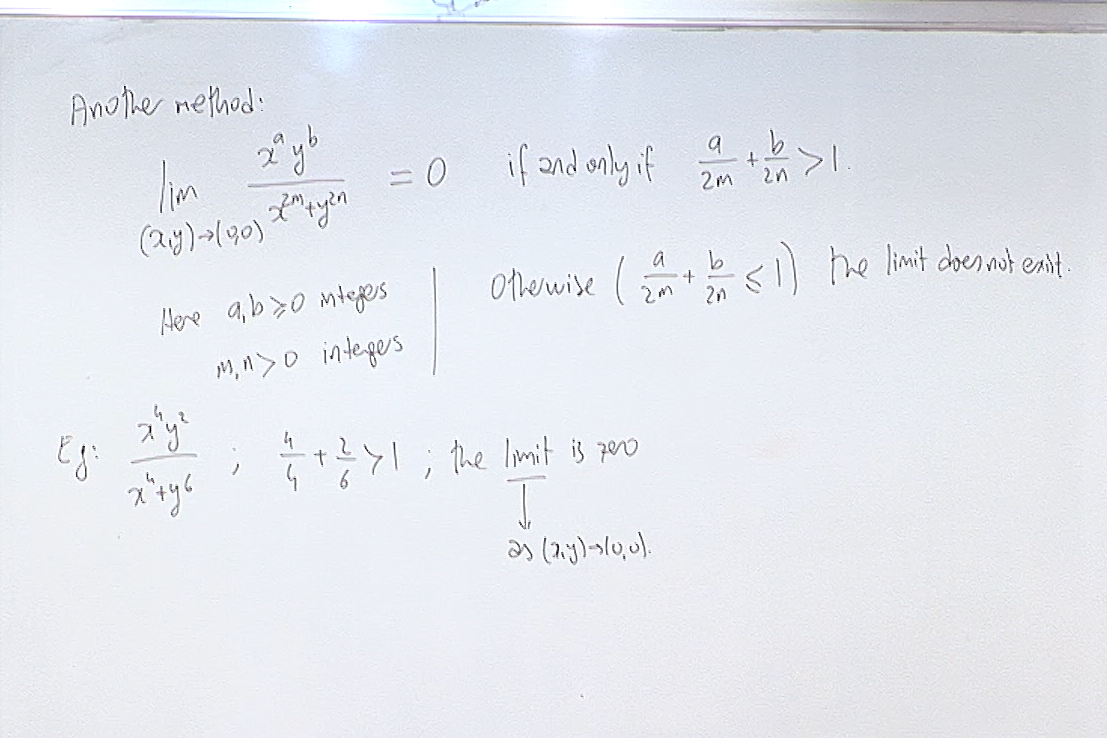
This "another method" is the so called Sertöz Theorem.

An application of the Sertöz Theorem.
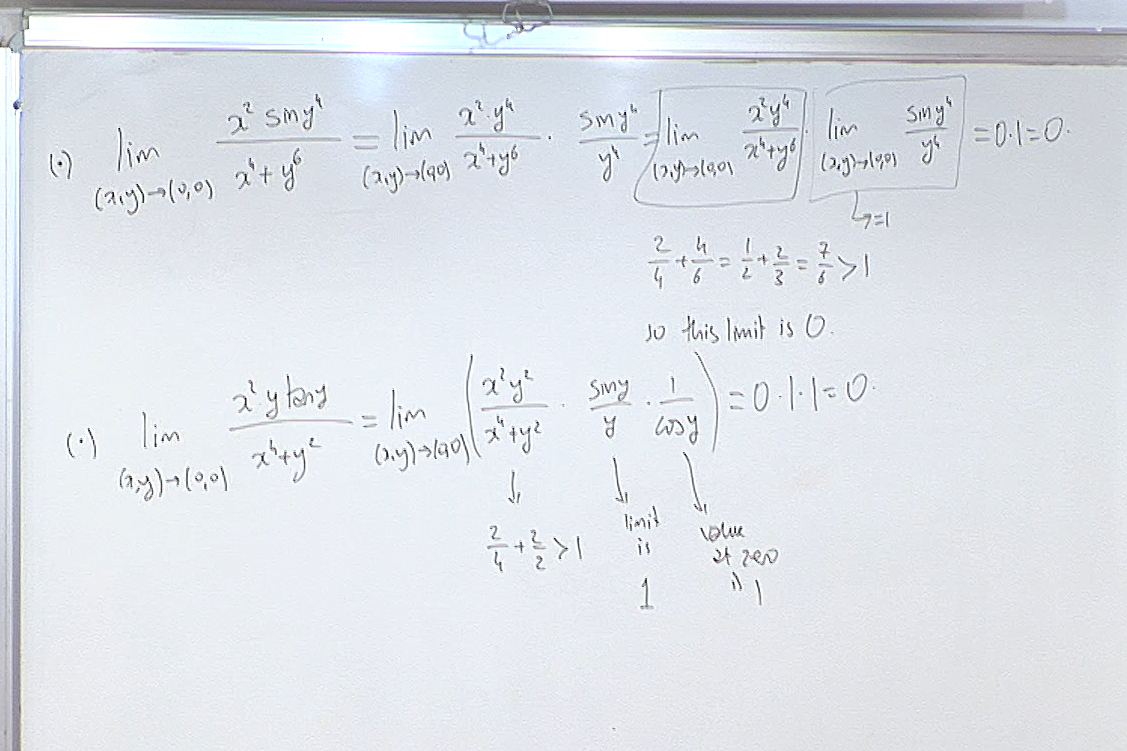
Another application of the Sertöz Theorem.

Notice that while taking partial derivatives at a point we approach that point along very special paths, namely paths parallel to the coordinate axes. Therefore these derivatives will not be as informative about the function as their one variable counterparts . But we will nonetheless manage to read off a lot of information about the function from its partial derivatives.

The mechanical way of taking a partial derivative with respect to a certain variable is to treat everything else as a constant, and use the rules for one variable case.
