
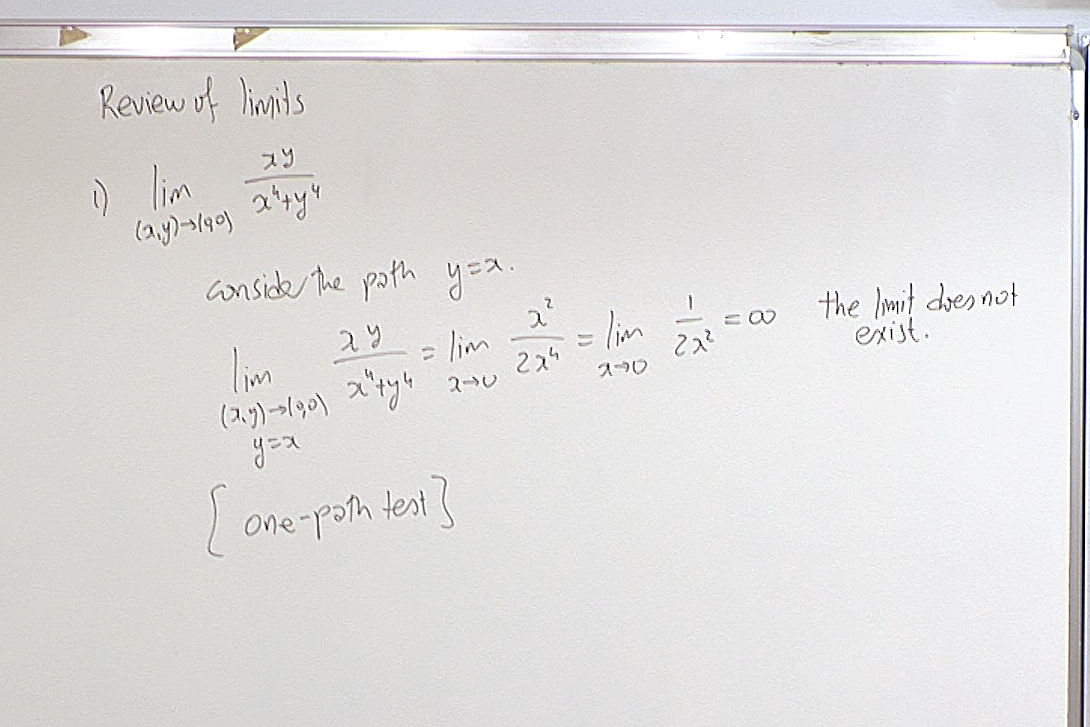
If the limit along one particular path is infinite, then the limit does not exist.
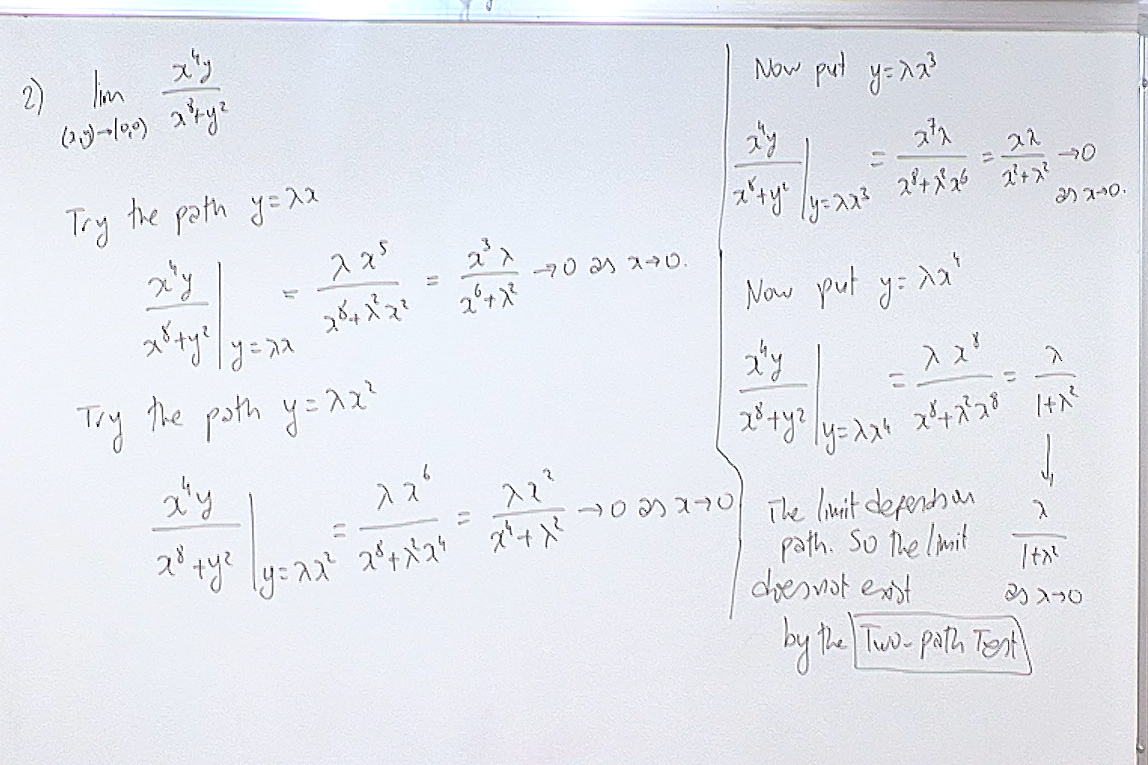
If the limits along several paths are the same, this does NOT guarantee that the actual limit exists. However if you find a path along which the limit is different than the ones you found before, then you conclude that the limit does not exist. In the above calculatin the fourth path gave us a different limit. Until then all we knew was that if the limit existed then it would be zero.

Sometimes changing to polar coordinates makes the calculations simpler. But make sure that the limit does not depend on the angle $\theta$.

Squeeze theorem is nice but you have to find an easy function which bounds your function.
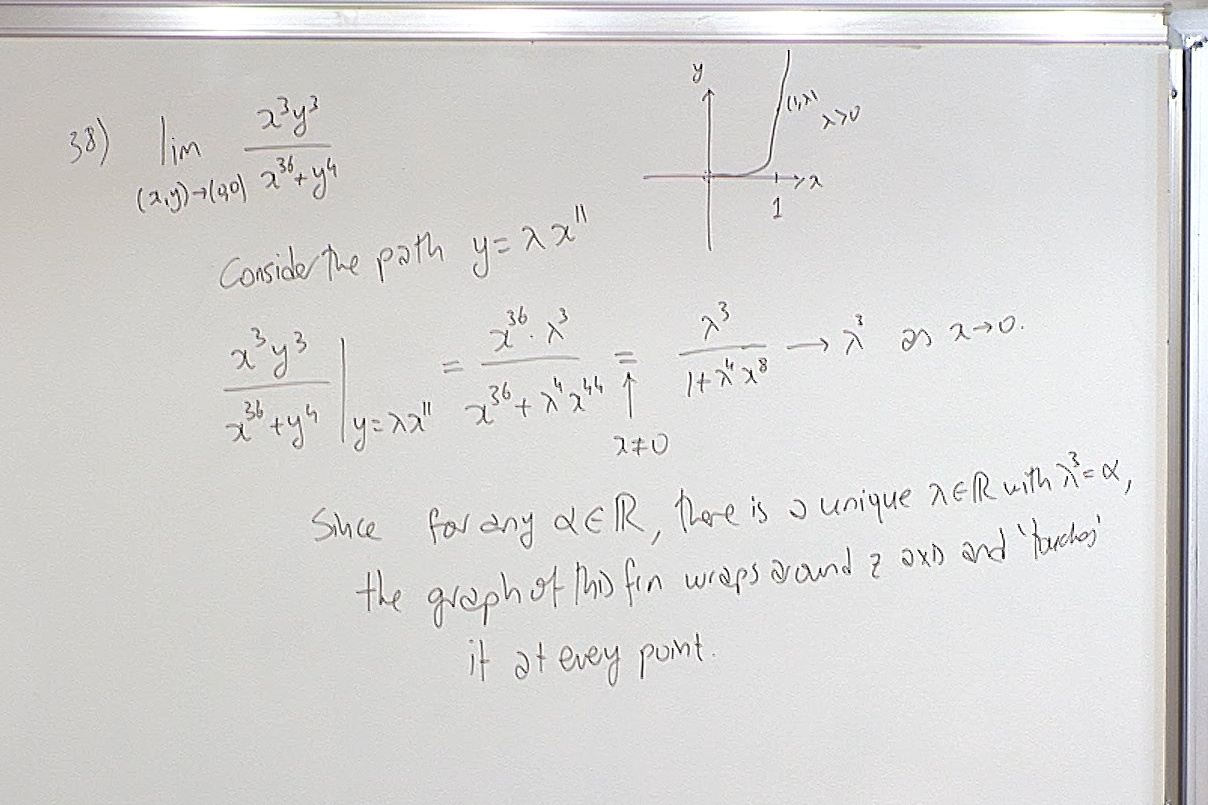
This answers the question "How bad can the singularity be?" Here the surface defined by $\displaystyle z=\frac{x^3y^3}{x^{36}+y^4}$ becomes arbitrarily close to every point of the $z$-axis. So the limit fails to exist miserably.
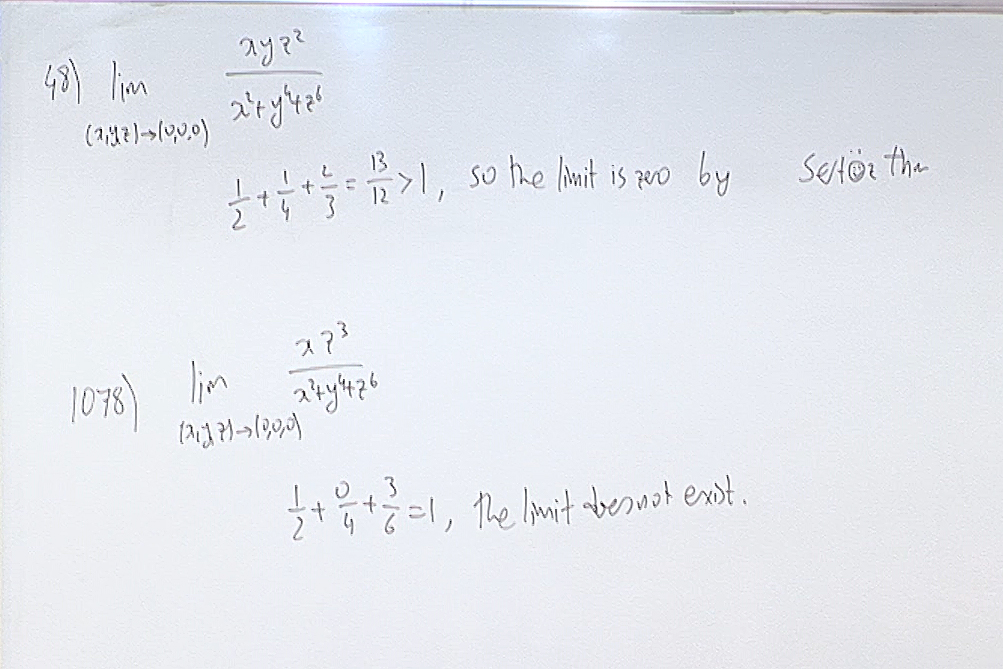
Probably the easiest way to determine if the limit exists: The Sertöz Theorem 
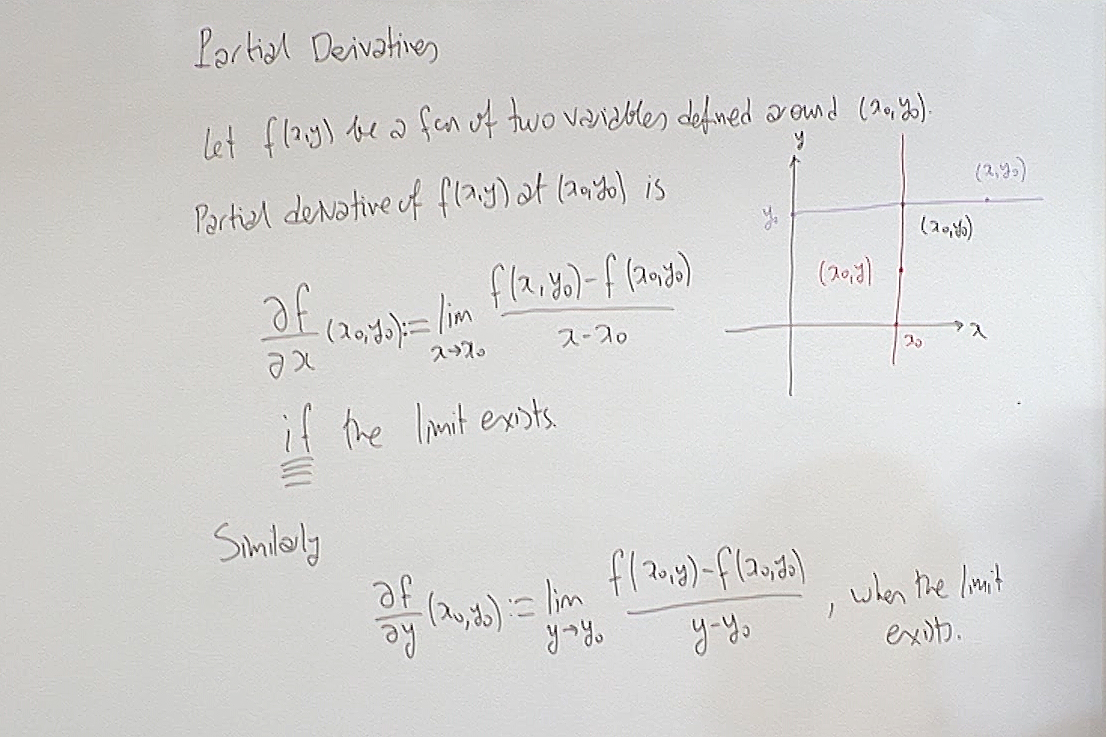
We now pass to a new topic: Partial Derivatives. Note that these are derivatives along special directions so will not be as informative as the derivative of a single variable function. Nonetheless thay carry sufficient information to deduce the essential nature of the function.
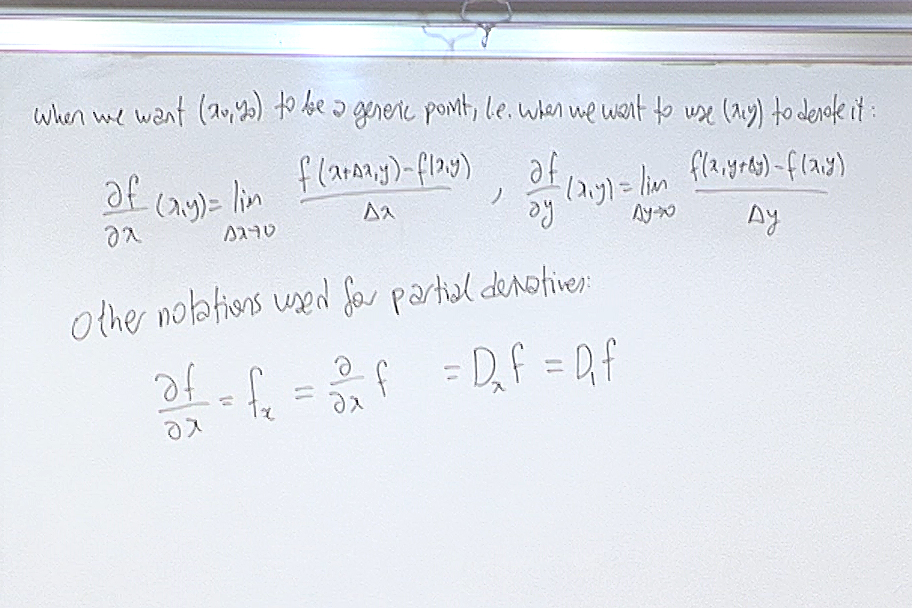
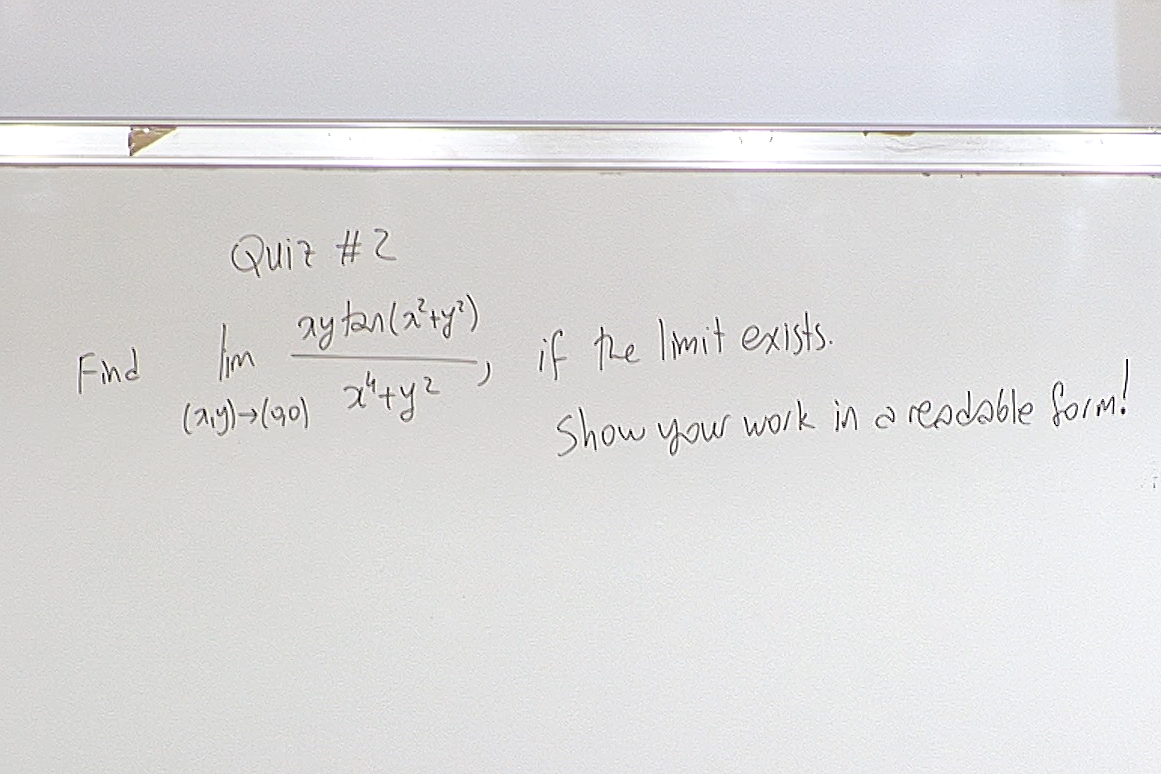
At this point we had a quiz. Here is the question.

