"What's in a name? That which we call a rose
By any other name would smell as sweet."

Romeo and Juliet (II, ii, 1-2)

Taylor's Theorem was stated in 1712 by  Brook Taylor (1685-1731), forty one years after it was originally announced in 1671 by James Gregory (1638-1675). And special cases were already known by Madhava of Sanyamagrama (1350-1425).

Of course Colin Maclaurin (1698-1746) did not discover the Maclaurin series. He discovered the integral test for the convergence of infinite series.

Gabriel Cramer (1704-1752) published Cramer's rule  two years after it was published by Colin Maclaurin.

Stokes' Theorem was not discovered by Gabriel Stokes (1819-1903) at all. It was discovered by William Thomson, a.k.a. Lord Kelvin (1824-1907).
[In fact my friend Okan Tekman informed me that this theorem has a longer and more convoluted history. See Okan's summary.]

Stirling's formula was not discovered by James Stirling (1692-1770) but was discovered by Abraham de Moivre (1667-1754).

So, before the historians come in, here is Sertoz Theorem:  

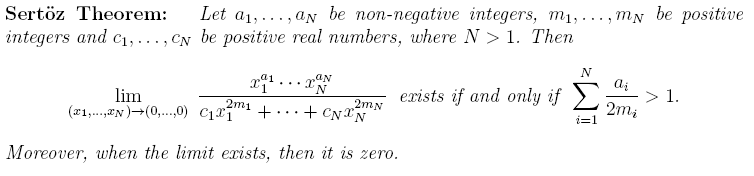
For the original proof of the theorem, follow this link. 

There is a wonderful and short proof thanks to Kocatepe.

Türkçe'si için buraya tıklayabilirsiniz.

---Here is an application:

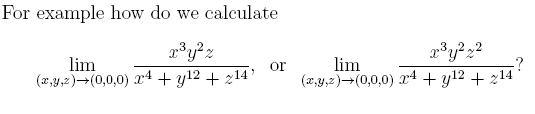
Here is the answer:

(3/4)+(2/12)+(1/14) = (83/84) < 1, so the first limit does not exist, but (3/4)+(2/12)+(2/14) = (89/84) > 1, so the second limit exists and is zero.

---