
Previous Screenshot Next Screenshot
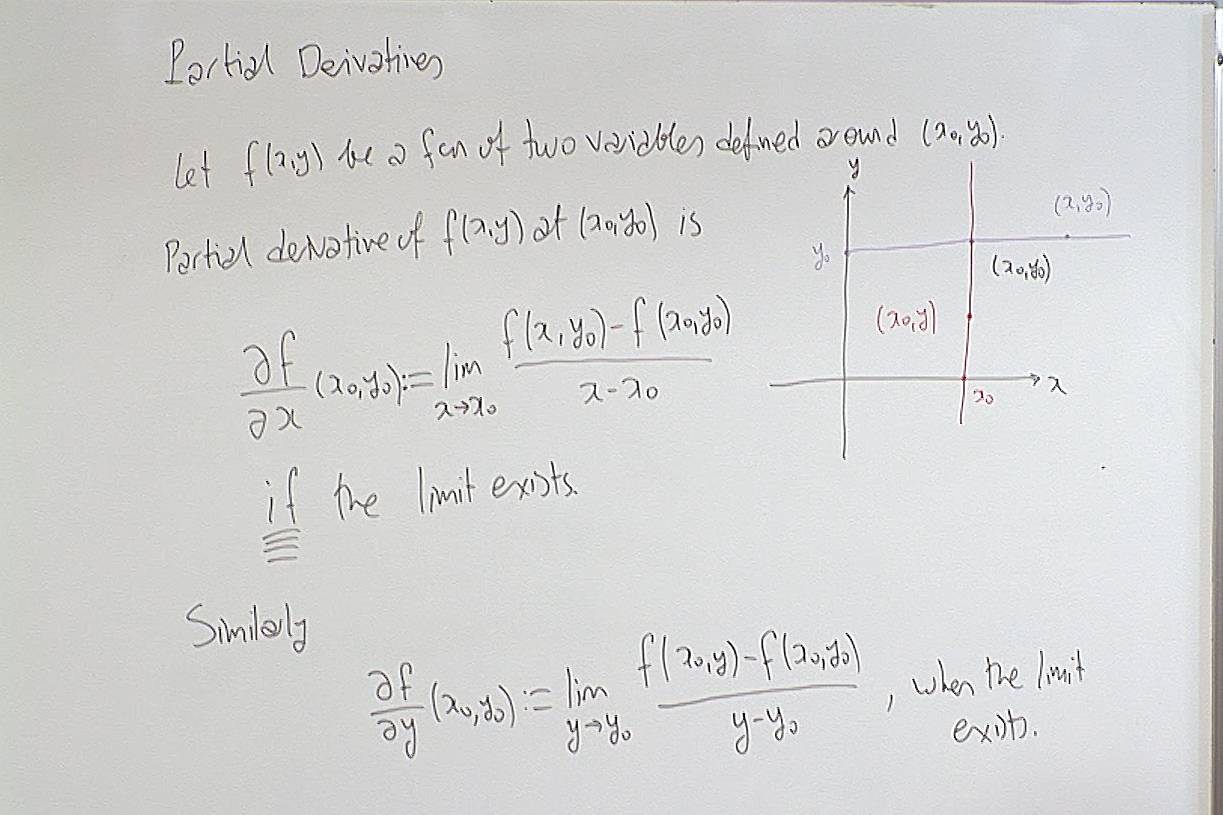
Notice that when we want to calculate the derivative of $f(x,y)$ with respect to $x$, we keep $y$ fixed. And similarly when we are calculating the derivative with respect to $y$, we keep the other variables, only $x$ in this case, fixed.

This explains the geometric interpretation of partial derivatives. Consider the plane $\pi$ perpendicular to the $xy$-plane along the line $y=y_0$. This plane intersects the surface $z=f(x,y)$ along the pruple curve given above. The slope of the tangent line to this curve at the point $x=x_0$ in the plane $\pi$ is the partial derivative of $f(x,y)$ at the point $(x_0,y_0)$. Similarly the partial derivative with respect to $y$ is interpreted as the slope of the red curve above at $y=y_0$, in another plane perpendicular to $xy$-plane along the curve $x=x_0$.

This shows that very bad functions can have partial derivatives. This is in contrast with the one variable case: if $f(x)$ has a derivative at $x_0$, then $f$ must be continuous at $x_0$. Not so for several variable case as the example above demonstrates.

The note on the top is about differentiability. We will come back to this later. First we consider higher derivatives.

This theorem tells us when mixed partial derivatives will be equal.

Here we find that \[ f_x(x,y)=\begin{cases} \frac{x^4y+4x^2y^3-y^5}{(x^2+y^2)^2} & (x,y)\not=(0,0) \\ 0 & (x,y)=(0,0) \end{cases} \] and \[ f_y(x,y)=\begin{cases} \frac{x^5-4x^3y^2-xy^4}{(x^2+y^2)^2} & (x,y)\not=(0,0) \\ 0 & (x,y)=(0,0) \end{cases} \] Now we calculate $f_{xy}(0,0)$ and $f_{yx}(0,0)$ using the above expressions. \begin{eqnarray*} f_{xy}(0,0) &=& \lim_{\Delta y\rightarrow 0} \frac{f_x(0,\Delta y)-f_x(0,0)}{\Delta y} \\ &=& \lim_{\Delta y\rightarrow 0} \frac{\frac{-(\Delta y)^5}{(\Delta y)^4}}{\Delta y} =-1. \end{eqnarray*} Whereas \begin{eqnarray*} f_{yx}(0,0) &=& \lim_{\Delta x\rightarrow 0} \frac{f_y(\Delta x,0)-f_y(0,0)}{\Delta x} \\ &=& \lim_{\Delta x\rightarrow 0} \frac{\frac{(\Delta x)^5}{(\Delta x)^4}}{\Delta x} =1. \end{eqnarray*} So we found that $f_{xy}(0,0)\not=f_{yx}(0,0)$.

We check that along every line $y=tx$, the mixed second derivatives have the same value depending on $t$. So the limit as $x\rightarrow 0$ along each line $y=tx$ is different. This says that $f_{xy}$ and $f_{yx}$ are not continuous at the origin. So the Clairaut theorem does not guarantee that they will be equal at the origin and in fact in this case they are different.
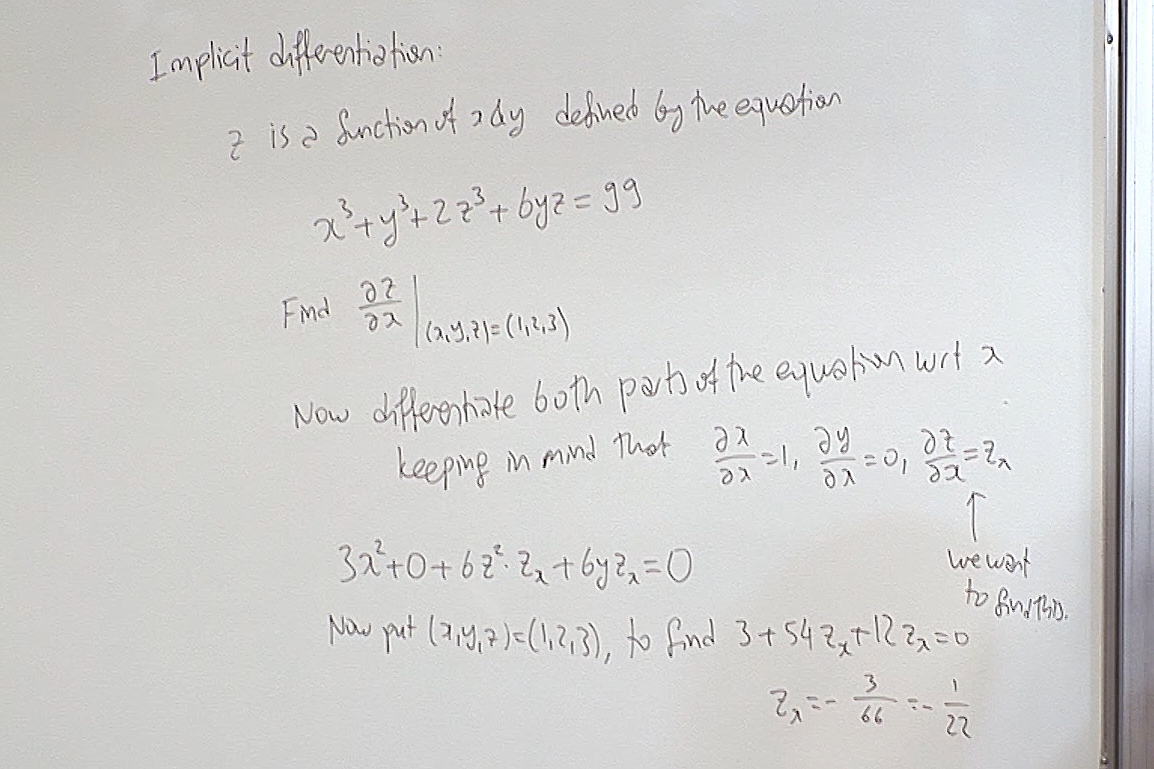
When three variables are related by an equation we must decide which two determines the other. The partial derivatives are then taken accordingly. In the above calculation we decided that $x$ and $y$ are free and determine $z$.

Here we consider again the equation \[ x^3+y^3+2z^3+6yz=99. \] Then we play a game! Fill out each box in the above table and see if you can spot a pattern. Here for example when you calculate in the first row $\frac{\partial y}{\partial x}$, you assume that $x$ and $z$ are free and determine $y$. Then evaluate at $(1,2,3)$. Interpret all the other boxes similarly. We will see the solution in the next day's screenshots.
