
Previous Screenshot Next Screenshot

Here we review the definition of partial derivatives.

We do an example and review implicit differentiation.

We finally come back to the problem we posed last hour. We have \[ F(x,y,z)=x^3+y^3+2z^3+6yz=99 \] defining a surface in $\mathbb{R}^3$. We want to fill the above table where the partial derivatives are evaluated at the point $(1,2,3)$. The first entry is $\displaystyle \frac{\partial y}{\partial x}(1,2,3)$. This means $y$ is treated as a function of $x$ and $z$ around the point $(1,2,3)$. In particular $x$ and $z$ are free variables so \[ \frac{\partial x}{\partial x}=1, \; \frac{\partial z}{\partial x}=0. \] Now implicitly differentiating $F(x,y,z)=99$ and putting in $(x,y,z)=(1,2,3)$, we get $\displaystyle \frac{\partial y}{\partial x}=-\frac{1}{10}$ as shown on the board. \\ Let us now calculate $\displaystyle \frac{\partial z}{\partial y}(1,2,3)$ to demonstrate the above procedure. Here note that $z$ is treated as a function of $x$ and $y$ around the point $(1,2,3)$. Hence in particular $x$ and $y$ are free so \[ \frac{\partial x}{\partial y}=0, \; \frac{\partial y}{\partial y}=1. \] Now implicitly differentiate $F(x,y,z)=99$ with respect to $y$ to get \[ 3y^2+6z^2\frac{\partial z}{\partial y}+6z+6y \frac{\partial z}{\partial y} =0. \] Now put $(x,y,z)=(1,2,3)$ and solve for $\displaystyle \frac{\partial z}{\partial y}(1,2,3)$ to get \[ \frac{\partial z}{\partial y}(1,2,3)=-\frac{5}{11}. \] The other entries are calculated similarly.
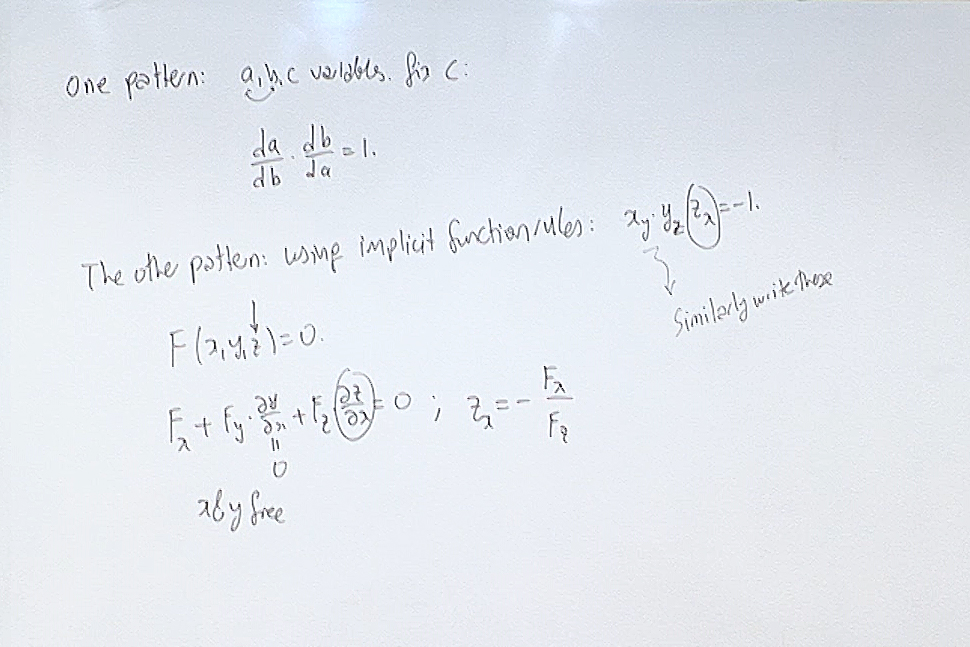
Now we start observing patterns on this table. \\ First observation is the implementation of chain rule to inverse functions. Let\[ y=f(x), \; \; x=f^{-1}(y). \] Then we have through chain rule \[ \frac{\partial x}{\partial y}\frac{\partial y}{\partial x}=1. \] The notation on the top of the board recalls this fact where we treat $a$ and $b$ as inverses of each other while fixing $c$. Here $a,b,c\in \{ x,y,z \} $.
The second pattern we observe is given below the first pattern on the board as \[ \frac{\partial x }{\partial y}\frac{\partial y}{\partial z }\frac{\partial z}{\partial x }=-1. \] Notice here that $\partial x$, $\partial y$ and $\partial z$ do not cancel as if they are independent variables! You calculate each partial derivative separately from $F(x,y,z)=99$ by implicit differentiation and then multiply them. On the board we demonstrate how to calculate $\displaystyle \frac{\partial z}{\partial x}$. The others are calculated similarly. Then we get \[ \frac{\partial x }{\partial y}\frac{\partial y}{\partial z }\frac{\partial z}{\partial x }=\left( -\frac{F_y}{F_x}\right) \left( -\frac{F_z}{F_y}\right) \left( -\frac{F_x}{F_z}\right)=-1. \]
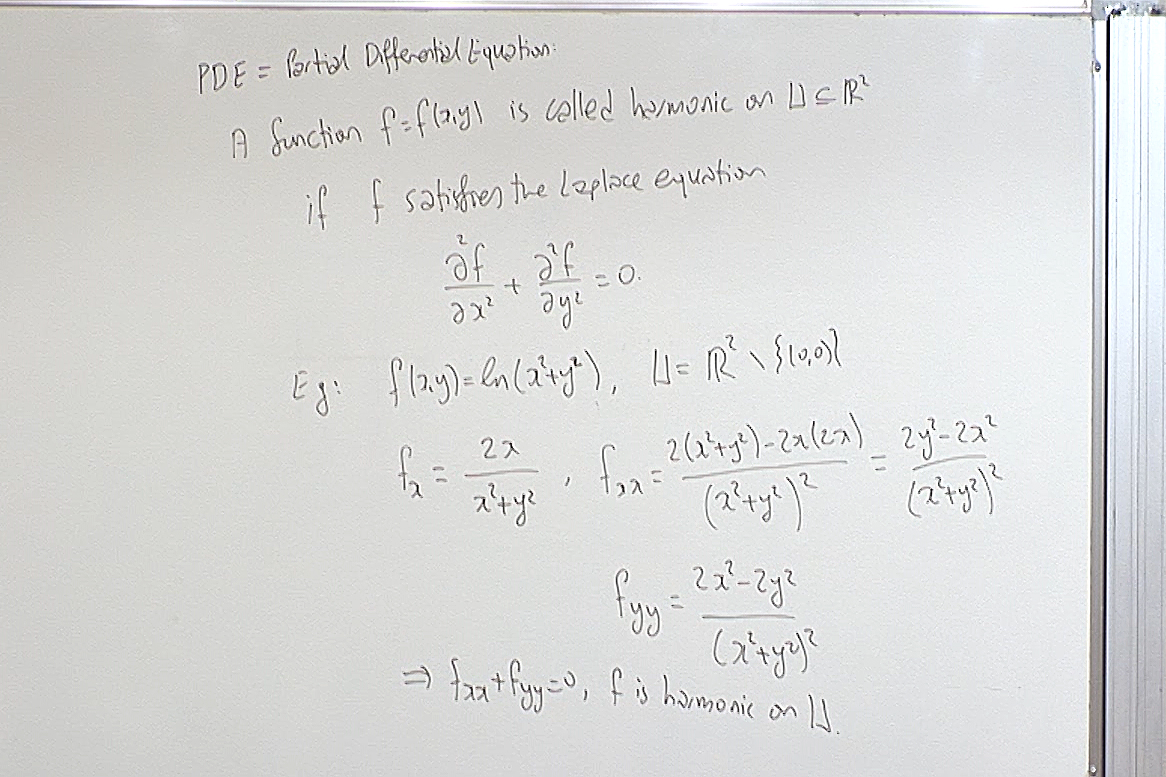
Definition of harmonic function in two variables.
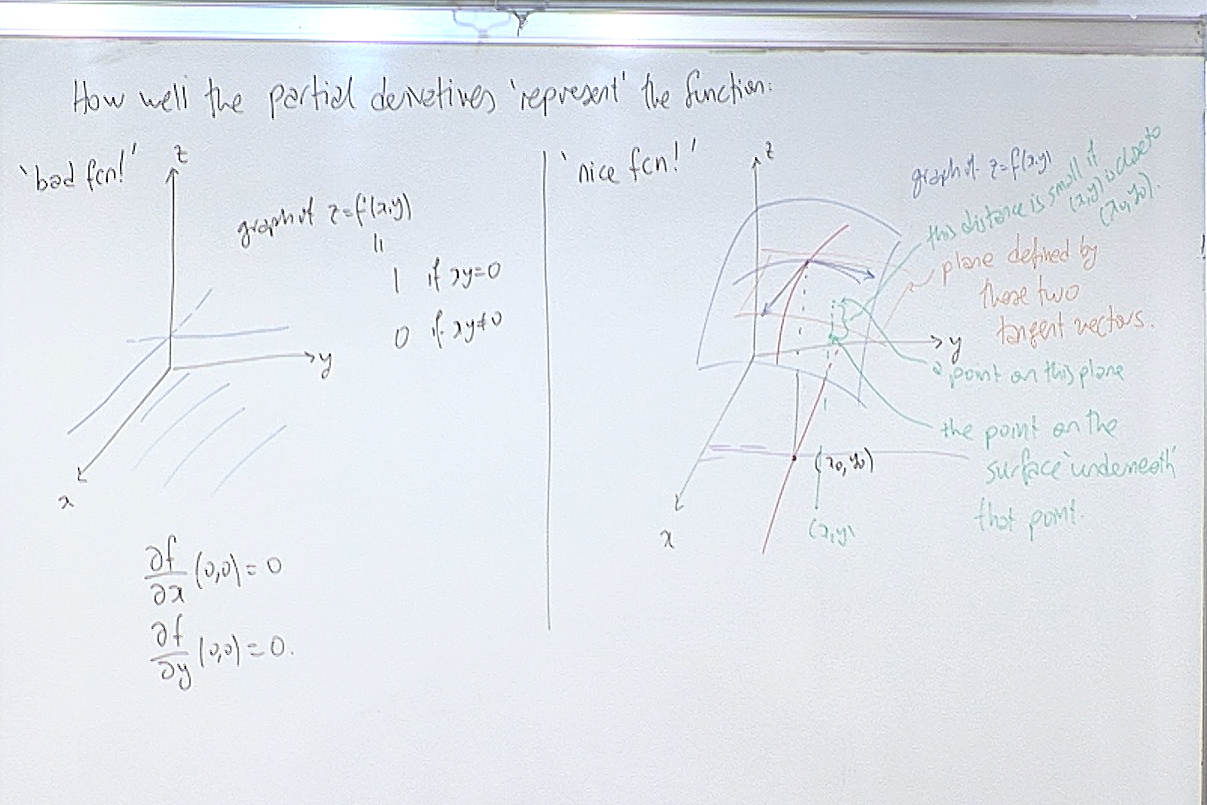
Partial derivatives only calculate the behavior of the function along lines parallel to the coordinate axes. Thus partial derivatives in general do not detect how the function behaves outside these lines. The example on the left shows a function whose partial derivateives at the origin exist but the function is not even continuous there. The function on the right is however "nice". How do we tell the difference?

To tell the difference between "nice" and "bad" we define differentiable function.
