
Previous Screenshot Next Screenshot

Recall the definition of differentiability from the previous hour. Here we show that a function of a single variable is differentiable if its derivative exists. This is not true for functions of more than one variable. The theorem above tells us how to recognize a differentiable function.

On the top right side of the board we give a symbolic picture showing that differentiable functions are very few compared to non-differentiable functions.

The proof of the theorem is given for completeness and to show that the result is not a miracle but follows from what we learned so far.
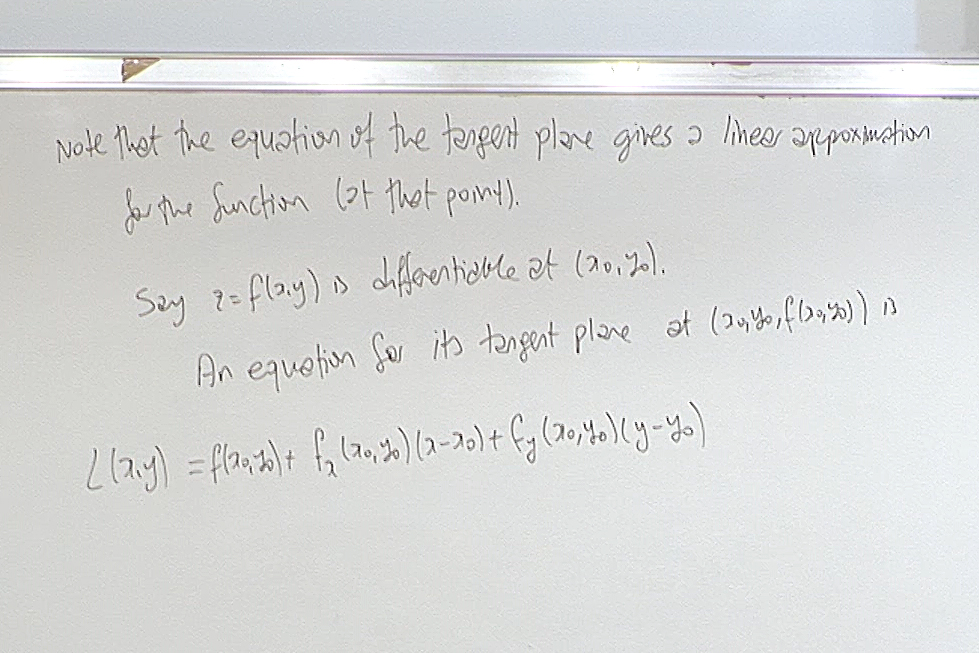
Linearization is defined for differentiable functions.
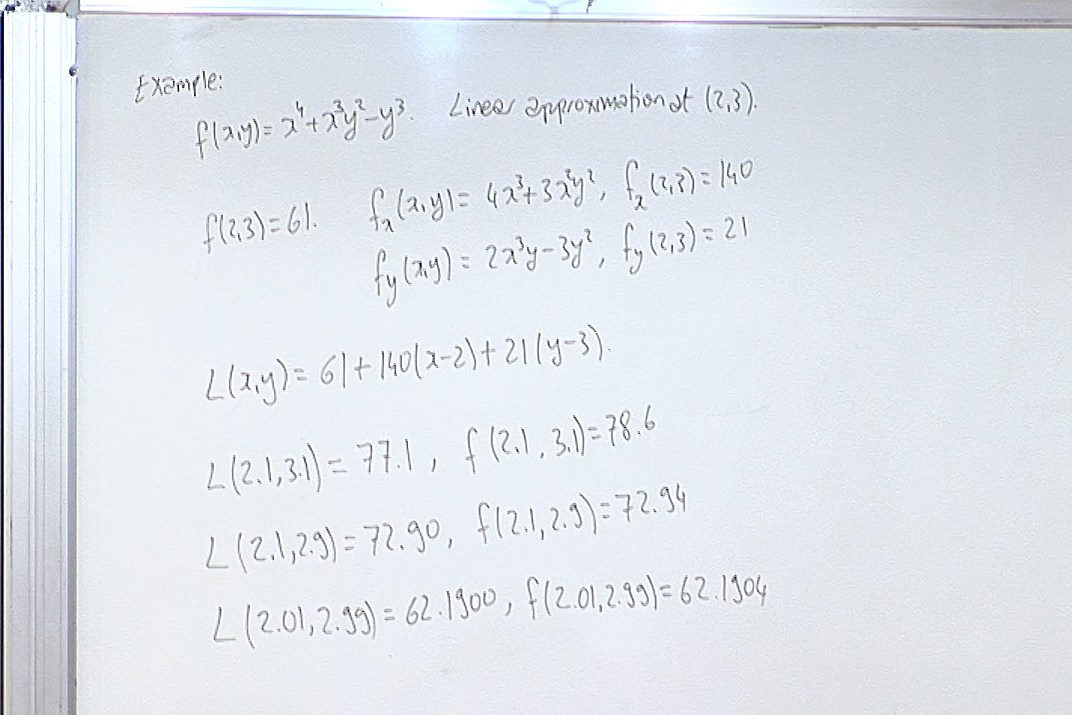

Here we explain the geometric meaning attached to differential symbol in calculus. It is basically the difference between the linearization and the actual value.


This is the main tool in calculating partial derivatives for complicated functions.
