
Previous Screenshot Next Screenshot

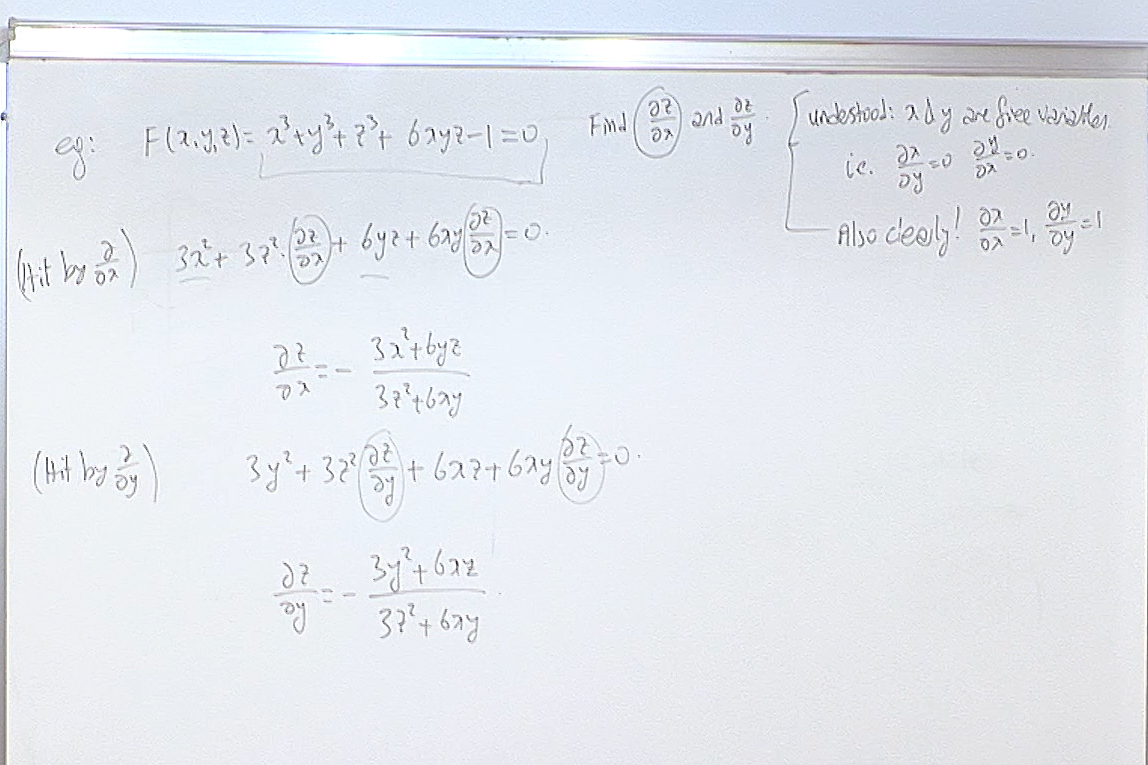
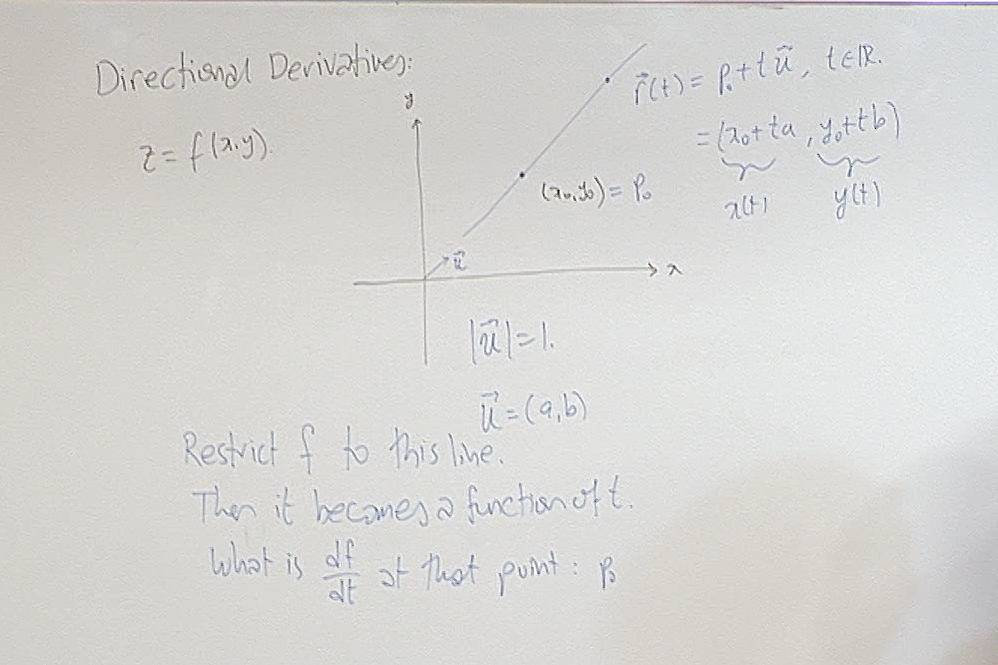




The last remark about finding the maximum is an approximate method when exact algebraic callculations are too complicated to try. The method works as follows. Suppose you want to find at which point a function $f$ of several variables takes its maximum value. First you make a guess $p_0$ and set a small constant $\epsilon>0$ depending on how close you want to approximate the maximum point. You calculate $\nabla f(p_0)$ and set $p_1=p_0+\epsilon \nabla f(p_0)$. Then you repeat the process starting at $p_1$. In general we get the point $p_n$ as $p_{n-1}+\epsilon \nabla f(p_{n-1})$. The sequence $p_0,p_1,\dots,p_n,\dots$ generally approaches to the maximal point.
