
Previous Screenshot Next Screenshot
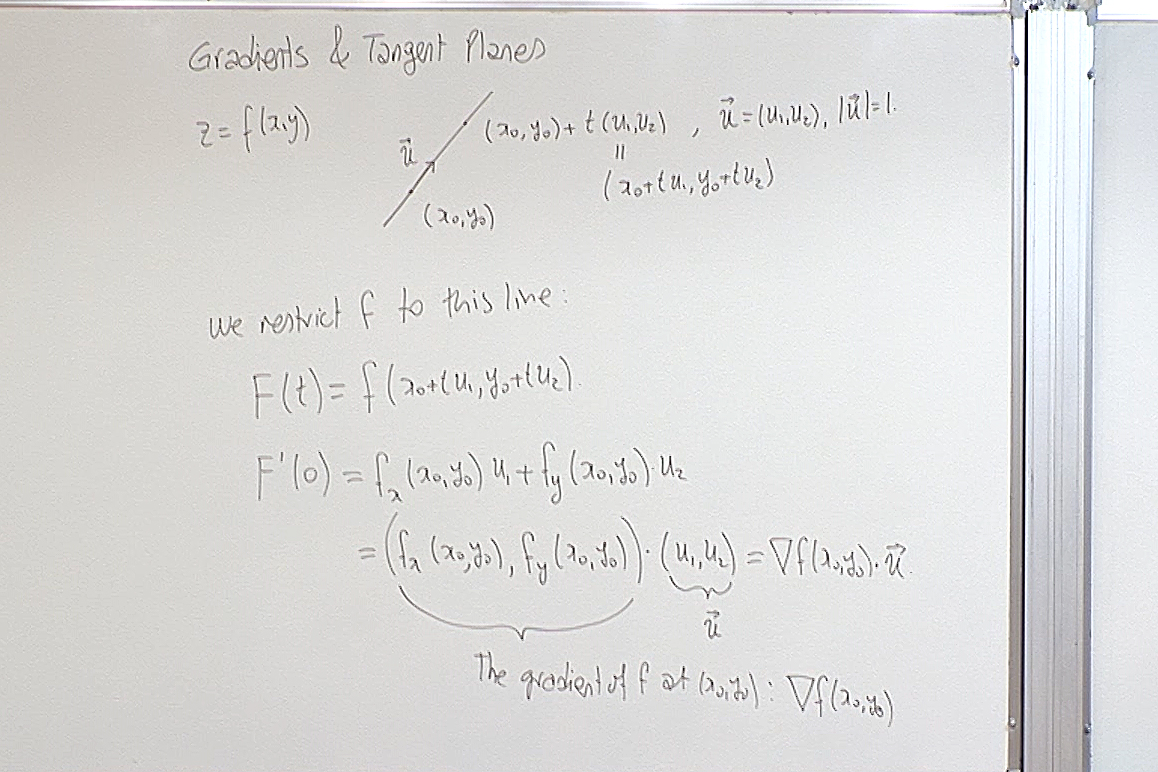


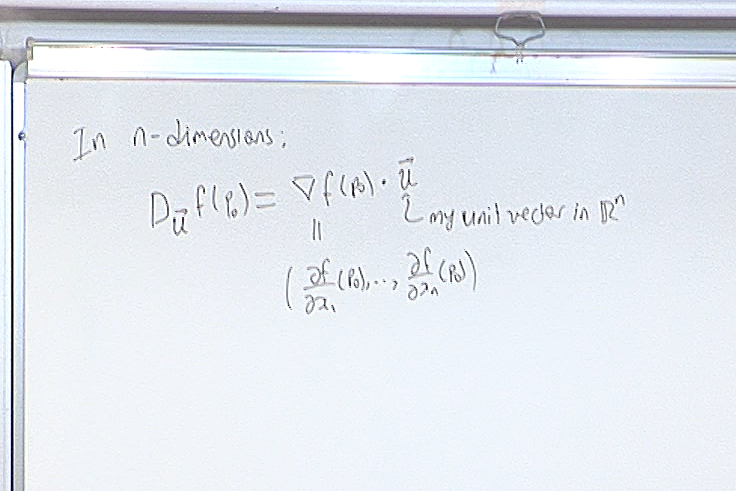

The circle example is to illustrate what generally happens. This circle if given by $F(x,y)=x^2+y^2-1$. Therefore it encodes the two functions $y=\pm \sqrt{1-x^2}$. Instead of trying to solve for these functions, take the derivative and then write the equation of the tangent line, the gradient technique gives information about the tangent line immediately.

In the example on the top right, the gradient vanishes at the origin and there the curve has a pinch. That is a "bad" point. The non-vanishing of the gradient guarantees that our geometric object is "nice".


